题目内容
在△ABC中，B=90°，AC=
，D、E两点分别在AB、AC上，使
=
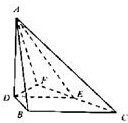
=2，DE=3，现将△ABC沿DE折成直二面角（如图所示）
求：（1）异面直线BC与AE所成角的余弦值
（2）二面角A-EC-B的正切值．
| 15 |
| 2 |
| AD |
| DB |
| AE |
| EC |
求：（1）异面直线BC与AE所成角的余弦值
（2）二面角A-EC-B的正切值．
考点：二面角的平面角及求法,异面直线及其所成的角
专题：综合题,空间位置关系与距离,空间角
分析：（1）证明DE∥BC，可得∠AED（或其补角）为异面直线BC与AE所成角；
（2）过D作DF⊥CE，交CE的延长线于F，先证得∠AFD为二面角A-BC-B的平面角，再利用直角三角形中的边角关系求出其正切值即得．
（2）过D作DF⊥CE，交CE的延长线于F，先证得∠AFD为二面角A-BC-B的平面角，再利用直角三角形中的边角关系求出其正切值即得．
解答：
解：（1）∵
=
=2，
∴DE∥BC，
∴∠AED（或其补角）为异面直线BC与AE所成角，
∵DE=3，AE=5，
∴cos∠AED=
；
（2）过D作DF⊥CE，交CE的延长线于F，连接AF．
∵A-DE-B是直二面角，AD⊥DE，∴AD⊥底面DBCE，
由三垂线定理知AF⊥FC，故∠AFD为二面角A-BC-B的平面角．
在底面DBCE中，∠DEF=∠BCE，DB=2，EC=
，
因此sinBCE=
=
．
从而在Rt△DFE中，DE=3，DF=DEsinDEF=DEsinBCE=
．
在Rt△AFD中，AD=4，tan∠AFD=
=
．
因此，二面角A-EC-B的正切值为
．
解：（1）∵| AD |
| DB |
| AE |
| EC |
∴DE∥BC，
∴∠AED（或其补角）为异面直线BC与AE所成角，
∵DE=3，AE=5，
∴cos∠AED=
| 3 |
| 5 |
（2）过D作DF⊥CE，交CE的延长线于F，连接AF．
∵A-DE-B是直二面角，AD⊥DE，∴AD⊥底面DBCE，
由三垂线定理知AF⊥FC，故∠AFD为二面角A-BC-B的平面角．
在底面DBCE中，∠DEF=∠BCE，DB=2，EC=
| 5 |
| 2 |
因此sinBCE=
| DB |
| EC |
| 4 |
| 5 |
从而在Rt△DFE中，DE=3，DF=DEsinDEF=DEsinBCE=
| 12 |
| 5 |
在Rt△AFD中，AD=4，tan∠AFD=
| AD |
| DF |
| 5 |
| 3 |
因此，二面角A-EC-B的正切值为
| 5 |
| 3 |
点评：本小题主要考查异面直线及其所成的角、二面角等基础知识，考查空间想象能力，运算能力和推理论证能力．
练习册系列答案
黄冈冠军课课练系列答案
相关题目
如图，在四棱锥P-ABCD中，底面ABCD为矩形，PA⊥底面ABCD，AP=AB=