题目内容
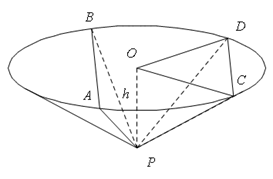
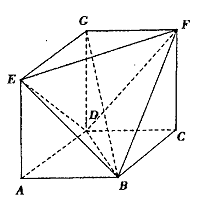
如图,在底面是正方形的四棱锥P—ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
(1)求证:BD⊥FG;
(2)确定点G在线段AC上的位置,使FG//平面PBD,并说明理由.
(3)当二面角B—PC—D的大小为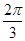 时,求PC与底面ABCD所成角的正切值.
时,求PC与底面ABCD所成角的正切值.
(1)根据题意,由于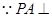 面ABCD,四边形ABCD是正方形,结合其性质可知PA⊥BD,AC⊥BD,进而得到证明。
面ABCD,四边形ABCD是正方形,结合其性质可知PA⊥BD,AC⊥BD,进而得到证明。
(2)当G为EC中点 (3)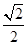
解析试题分析:解:方法一:(I)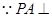 面ABCD,四边形ABCD是正方形,
面ABCD,四边形ABCD是正方形,
其对角线BD,AC交于点E,∴PA⊥BD,AC⊥BD
∴BD⊥平面APC, 平面PAC,
平面PAC,
∴BD⊥FG 3分
(II)当G为EC中点,即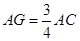 时,FG//平面PBD, 4分
时,FG//平面PBD, 4分
理由如下:
连接PE,由F为PC中点,G为EC中点,知FG//PE,
而FG 平面PBD,PB
平面PBD,PB 平面PBD, 故FG//平面PBD. 7分
平面PBD, 故FG//平面PBD. 7分
(III)作BH⊥PC于H,连结DH,
∵PA⊥面ABCD,四边形ABCD是正方形,
∴PB=PD,
又∵BC=DC,PC=PC,
∴△PCB≌△PCD,
∴DH⊥PC,且DH=BH,
∴∠BHD主是二面角B—PC—D的平面角, 9分
即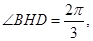
∵PA⊥面ABCD,
∴∠PCA就是PC与底面ABCD所成的角 10分
连结EH,则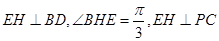
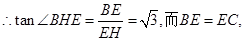
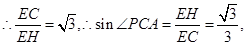
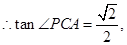
∴PC与底面ABCD所成角的正切值是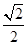 …………12分
…………12分
方法二解:以A为原点,AB,AD,PA所在的直线分别为x,y,z轴建立空间直角坐标系如图所示,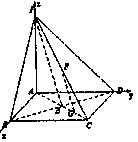
设正方形ABCD的边长为1,则A(0,0,0),B(1,0,0),C(1,1,0)
D(0,1,0),P(0,0,a)(a>0),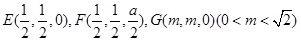
(I)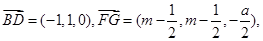
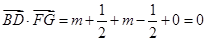
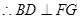 …………3分
…………3分
(II)要使FG//平面PBD,只需FG//EP,
而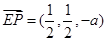 ,
,
由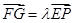 可得
可得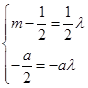 ,解得
,解得
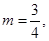 …………6分
…………6分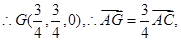
故当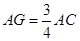 时,FG//平面PBD …………7分
时,FG//平面PBD …………7分
设平面PBC的一个法向量为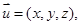
则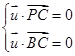 ,而
,而
 ,取z=1,得
,取z=1,得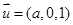 ,
,
同理可得平面PBC的一个法向量
设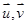 所成的角为0,
所成的角为0,
则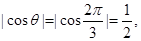
即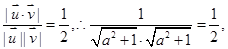
 …………10分
…………10分
∵PA⊥面ABCD,∴∠PCA就是PC与底面ABCD所成的角,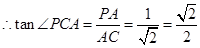
∴PC与底面ABCD所成角的正切值是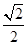 …………12分
…………12分
考点:空间中的线面角以线线垂直的证明
点评:主要是考查了空间中的线线以及线面的位置关系的运用,以及线面角的求解,属于中档题。

 中,
中,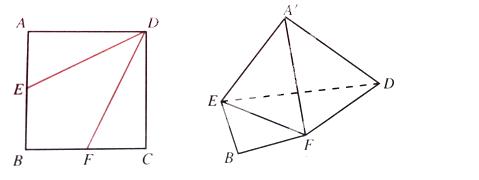
 是
是 的中点,点
的中点,点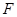 是
是 的中点,将
的中点,将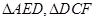 分别沿
分别沿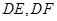 折起,使
折起,使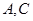 两点重合于点
两点重合于点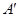 。求证:
。求证:
 时,求三棱锥
时,求三棱锥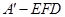 的体积。
的体积。
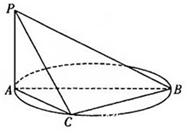
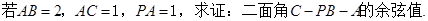
 .底面圆心为
.底面圆心为 ,其母线与底面所成的角为
,其母线与底面所成的角为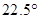 .
. 和
和 是底面圆
是底面圆 与平面
与平面 所成的角为
所成的角为 ,
, 
 与平面
与平面 .
.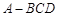 中,
中,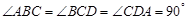 ,
,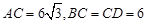 ,设顶点
,设顶点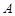 在底面
在底面 上的射影为
上的射影为 .
.
 ;
;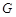 在棱
在棱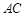 上,且
上,且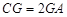 ,试求二面角
,试求二面角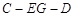 的余弦值.
的余弦值.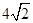 ,求二面角S-AB-C的余弦值。
,求二面角S-AB-C的余弦值。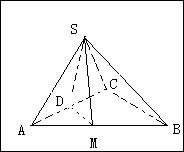
 ⊥平面
⊥平面 ,
,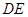 ∥
∥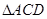 是正三角形,
是正三角形,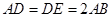 ,且
,且 是
是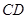 的中点.
的中点.
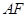 ∥平面
∥平面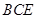 ;
; .
.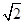 。
。
 的值;若不存在,说明理由.
的值;若不存在,说明理由. 的三视图,正(主)视图和俯视图都是矩形,侧(左)视图为等边三角形,
的三视图,正(主)视图和俯视图都是矩形,侧(左)视图为等边三角形, 为
为 的中点.
的中点.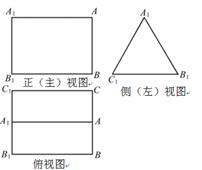
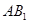 ∥平面
∥平面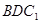 ;
;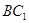 ,且
,且 ,求点
,求点 到平面
到平面 的距离.
的距离.