题目内容
某工厂某种产品的年固定成本为250万元,每生产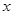 千件,需另投入成本为
千件,需另投入成本为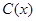 ,当年产量不足80千件时,
,当年产量不足80千件时,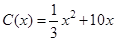 (万元).当年产量不小于80千件时,
(万元).当年产量不小于80千件时, (万元).每件商品售价为500元.通过市场分析,该厂生产的商品能全部售完.
(万元).每件商品售价为500元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润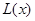 (万元)关于年产量
(万元)关于年产量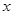 (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
(1) ;(2)当
;(2)当 时,即
时,即 时
时 取得最大值1000万元.
取得最大值1000万元.
解析试题分析:
对于有关利润的题目,要注意总销售额、成本,利润=总销售额-总成本,在题目中,如果含有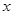 的范围有几段,则要分论,函数写成分段函数形式;则由题知每件商品售价为0.05万元,则
的范围有几段,则要分论,函数写成分段函数形式;则由题知每件商品售价为0.05万元,则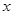 千件商品销售额为
千件商品销售额为 万元,在
万元,在 时,年利润
时,年利润 ;在
;在 ,年利润
,年利润 ,整理好结果用分段函数表示;(2)求利润最大,即是求函数的最大值,由于是分段函数,则分别求出每段函数的最大值,最终比较两段最大中的较大者,即是函数最大;由(1)可求
,整理好结果用分段函数表示;(2)求利润最大,即是求函数的最大值,由于是分段函数,则分别求出每段函数的最大值,最终比较两段最大中的较大者,即是函数最大;由(1)可求 则在
则在 时用二次函数的方法求最大,注意
时用二次函数的方法求最大,注意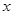 的范围,在
的范围,在 中,利用均值不等式求出,注意等号成立的条件.
中,利用均值不等式求出,注意等号成立的条件.
试题解析:(1)由题知每件商品售价为0.05万元,则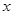 千件商品销售额为
千件商品销售额为 万元,
万元,
当 时,年利润
时,年利润 ;
;
当 ,年利润
,年利润 ,
,
则
(2)当 时,
时, 此时,当
此时,当 时,
时, 取得最大值
取得最大值 万元. 当
万元. 当 时,
时,  ,当
,当 时,即
时,即 时
时 取得最大值1000万元.
取得最大值1000万元.  ,所以,当产量为100千件时,该厂在这一商品中所获利润最大,最大利润为1000万元.
,所以,当产量为100千件时,该厂在这一商品中所获利润最大,最大利润为1000万元.
考点:1.函数的实际应用,2.分段函数的解析式的求法,3.分段函数最大值的求解.

练习册系列答案
相关题目
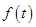 (单位:米)与生长年限t(单位:年)
(单位:米)与生长年限t(单位:年)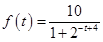 .(设该生物出生时t=0)
.(设该生物出生时t=0)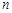 个工作台,将工艺流水线用如图
个工作台,将工艺流水线用如图 所示的数轴表示,各工作台的坐标分别为
所示的数轴表示,各工作台的坐标分别为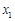 ,
,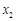 ,
,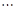 ,
,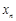 ,每个工作台上有若干名工人.现要在流水线上建一个零件供应站,使得各工作台上的所有工人到供应站的距离之和最短.
,每个工作台上有若干名工人.现要在流水线上建一个零件供应站,使得各工作台上的所有工人到供应站的距离之和最短.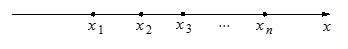
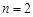 ,每个工作台上只有一名工人,试确定供应站的位置;
,每个工作台上只有一名工人,试确定供应站的位置;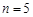 ,工作台从左到右的人数依次为
,工作台从左到右的人数依次为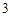 ,
,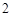 ,
,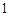 ,
, ,按每年
,按每年 衰减.
衰减. 年后,这种放射性元素的质量
年后,这种放射性元素的质量 与
与 的函数关系式;
的函数关系式; 时所经历的时间).(
时所经历的时间).( )
) 是一个矩形花坛,其中AB=4米,AD=3米.现将矩形花坛
是一个矩形花坛,其中AB=4米,AD=3米.现将矩形花坛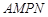 ,要求:B在
,要求:B在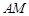 上,D在
上,D在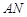 上,对角线
上,对角线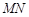 过C点,且矩形
过C点,且矩形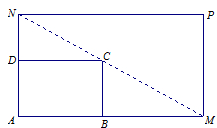
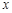 米,矩形
米,矩形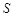 平方米,试用解析式将
平方米,试用解析式将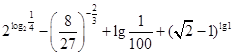
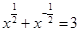 ,求
,求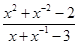 的值.
的值.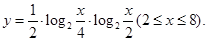
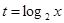 ,求
,求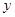 关于
关于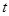 的函数关系式及
的函数关系式及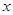 的值.
的值.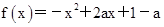 在
在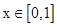 时有最大值2,求a的值.
时有最大值2,求a的值. 的定义域为
的定义域为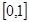 ,且同时满足以下三个条件:①
,且同时满足以下三个条件:①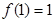 ;②对任意的
;②对任意的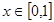 ,都有
,都有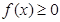 ;③当
;③当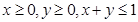 时总有
时总有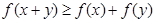 .
.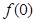 的值;
的值;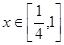 时,恒有
时,恒有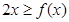 .
.