题目内容
已知函数 的定义域为
的定义域为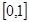 ,且同时满足以下三个条件:①
,且同时满足以下三个条件:①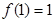 ;②对任意的
;②对任意的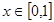 ,都有
,都有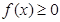 ;③当
;③当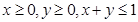 时总有
时总有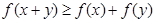 .
.
(1)试求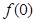 的值;
的值;
(2)求 的最大值;
的最大值;
(3)证明:当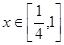 时,恒有
时,恒有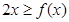 .
.
(1)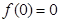 ;(2)
;(2)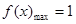 ;(3)
;(3)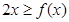 .
.
解析试题分析:(1)抽象函数求在特殊点的值,一般用赋值法,令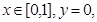 代入抽象函数可得
代入抽象函数可得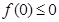 ,又因为
,又因为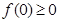 ,可得
,可得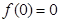 .(2)在定义域内求抽象函数最值,一般先判断函数单调性,再求比较定义域端点的函数值和极值点的大小.证明单调性可令
.(2)在定义域内求抽象函数最值,一般先判断函数单调性,再求比较定义域端点的函数值和极值点的大小.证明单调性可令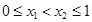 ,代入得
,代入得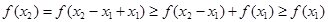 进而得函数为增函数,最大值为
进而得函数为增函数,最大值为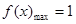 ;
;
(3)在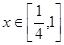 上证不等式
上证不等式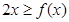 ,要分两段
,要分两段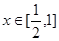 、
、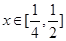 .在
.在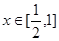 上
上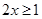 ,
,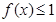 ,所以
,所以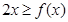 .在
.在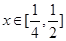
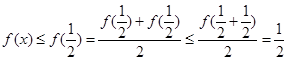 ,
,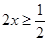 ,所以
,所以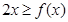 ,进而得证.
,进而得证.
试题解析:(1)令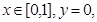 则有
则有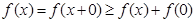 ,所以有
,所以有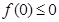 ,有根据条件?可知
,有根据条件?可知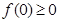 ,故
,故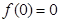 .(也可令
.(也可令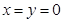 )
)
方法一:设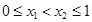 ,则有
,则有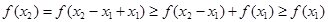 ,即
,即 为增函数(严格来讲为不减函数),所以
为增函数(严格来讲为不减函数),所以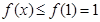 ,故
,故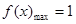 .
.
方法二:不妨令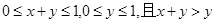 ,所以由?
,所以由? ,即
,即 增函数(严格来讲为不减函数),所以
增函数(严格来讲为不减函数),所以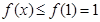 ,故
,故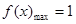 .
.
(3)当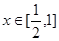 ,有
,有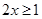 ,又由?可知
,又由?可知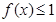 ,所以有
,所以有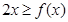 对任意的
对任意的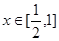 恒成立.当
恒成立.当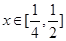 ,又由?可知
,又由?可知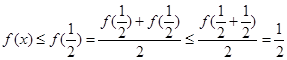 ,所以有
,所以有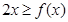 对任意的
对任意的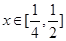 恒成立.综上,对任意的
恒成立.综上,对任意的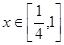 时,恒有
时,恒有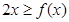 .
.
考点:1.抽象函数求值和单调性;2.证明不等式.

练习册系列答案
相关题目
 千件,需另投入成本为
千件,需另投入成本为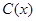 ,当年产量不足80千件时,
,当年产量不足80千件时,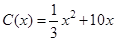 (万元).当年产量不小于80千件时,
(万元).当年产量不小于80千件时, (万元).每件商品售价为500元.通过市场分析,该厂生产的商品能全部售完.
(万元).每件商品售价为500元.通过市场分析,该厂生产的商品能全部售完.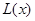 (万元)关于年产量
(万元)关于年产量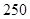 万元,每生产
万元,每生产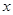 千件,需另投入成本为
千件,需另投入成本为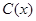 .当年产量不足
.当年产量不足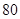 千件时,
千件时,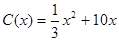 (万元).当年产量不小于
(万元).当年产量不小于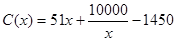 (万元).每件商品售价为
(万元).每件商品售价为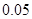 万元.通过市场分析,该厂生产的商品能全部售完.
万元.通过市场分析,该厂生产的商品能全部售完.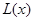 (万元)关于年产量
(万元)关于年产量
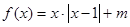
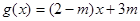 ,若方程
,若方程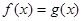 在
在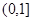 上有且仅一个实根,求实数
上有且仅一个实根,求实数 的取值范围;
的取值范围;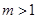 时,求函数
时,求函数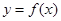 在
在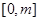 上的最大值.
上的最大值.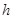 m,盖子边长为
m,盖子边长为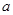 m,
m,
 .
. 时,求
时,求 的值域;
的值域; ,当
,当 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.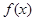 若存在
若存在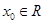 ,使得
,使得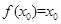 成立,则称
成立,则称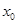 为
为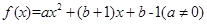
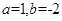 时,求函数
时,求函数 的不动点;
的不动点;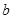 ,函数
,函数 的取值范围;
的取值范围;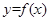 图象上
图象上 、
、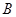 两点的横坐标是函数
两点的横坐标是函数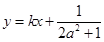 对称,求
对称,求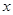 (元)与年产量
(元)与年产量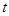 (吨)满足函数关系
(吨)满足函数关系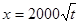 .若工厂每生产一吨产品必须赔付农场
.若工厂每生产一吨产品必须赔付农场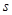 元(以下称
元(以下称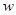 (元)表示为年产量
(元)表示为年产量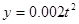 (元),在工厂按照获得最大利润的产量进行生产的前提下,农场要在索赔中获得最大净收入,应向张林的工厂要求赔付价格
(元),在工厂按照获得最大利润的产量进行生产的前提下,农场要在索赔中获得最大净收入,应向张林的工厂要求赔付价格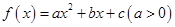 ,当
,当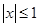 时,
时,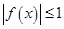 .
.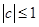 ;
;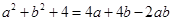 成立,请先求出
成立,请先求出 的值,并利用
的值,并利用 的表达式.
的表达式.