题目内容
17.已知双曲线M:x2-$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的左、右焦点分别为F1,F2,过点F1与双曲线的一条渐近线平行的直线与另一条渐近线交于点P,若点P在以原点为圆心,双曲线M的虚轴长为半径的圆内,则b2的取值范围是( )| A. | (7+4$\sqrt{3}$,+∞) | B. | (7-4$\sqrt{3}$,+∞) | C. | (7-4$\sqrt{3}$,7+4$\sqrt{3}$) | D. | (0,7-4$\sqrt{3}$)∪(7+4$\sqrt{3}$,+∞) |
分析 根据双曲线渐近线的方程求出交点P的坐标,结合点与圆的关系建立不等式关系进行求解即可.
解答 解:过F1(-c,0)且与渐近线y=bx平行的直线为y=b(x+c),
与另外一条渐近线y=-bx联立得$\left\{\begin{array}{l}{y=b(x+c)}\\{y=-bx}\end{array}\right.$,得$\left\{\begin{array}{l}{x=-\frac{c}{2}}\\{y=\frac{bc}{2}}\end{array}\right.$,即P(-$\frac{c}{2}$,$\frac{bc}{2}$),
以原点为圆心,双曲线M的虚轴长为半径的圆的方程为x2+y2=4b2,
∴(-$\frac{c}{2}$)2+($\frac{bc}{2}$)2<4b2,即c2+b2c2<16b2,
把c2=b2+1代入并整理得b4-14b2+1<0,
得7-4$\sqrt{3}$<b2<7+4$\sqrt{3}$,
即b2的取值范围是(7-4$\sqrt{3}$,7+4$\sqrt{3}$),
故选:C
点评 本题主要考查双曲线的方程和性质,根据渐近线方程求出交点坐标,结合点与圆的位置关系建立不等式关系是解决本题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目
7.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的一个实轴端点与恰与抛物线y2=-4x的焦点重合,且双曲线的离心率等于2,则该双曲线的方程为( )
| A. | $\frac{x^2}{4}-\frac{y^2}{12}=1$ | B. | $\frac{x^2}{12}-\frac{y^2}{4}=1$ | C. | $\frac{x^2}{3}-\frac{y^2}{1}=1$ | D. | ${x^2}-\frac{y^2}{3}=1$ |
9.已知三棱锥S-ABC的所有顶点都在球O的球面上,球O的表面积为16π,△ABC是边长为3的正三角形,若SC⊥AB,SA⊥BC,则三棱锥S-ABC的体积的最大值为( )
| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{3\sqrt{3}}{4}$ | C. | $\frac{9\sqrt{3}}{4}$ | D. | $\frac{27\sqrt{3}}{4}$ |
6.双曲线$\frac{{x}^{2}}{3}$-y2=1的焦点F到其渐近线的距离为( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | 1 | C. | $\sqrt{3}$ | D. | 2 |
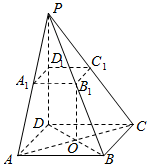 在四棱锥P-ABCD中,底面ABCD是菱形,PD⊥平面ABCD,点D1为棱PD的中点,过D1作与平面ABCD平行的平面与棱PA,PB,PC相交于A1,B1,C1,∠BAD=60°.
在四棱锥P-ABCD中,底面ABCD是菱形,PD⊥平面ABCD,点D1为棱PD的中点,过D1作与平面ABCD平行的平面与棱PA,PB,PC相交于A1,B1,C1,∠BAD=60°.