题目内容
15．函数f（x）=$\left\{{\begin{array}{l}{{x^2}+2x+2（x＜0）}\\{-{x^2}（x≥0）}\end{array}}\right.$，若f（f（a））=2，则a=$\sqrt{2}$．分析 当f（a）≥0时，f（f（a））=-[f（a）]2=2，不成立；当f（a）＜0时，f（f（a））=（f（a））2+2f（a）+2=2，解得f（a）=0（舍），或f（a）=-2，故f（a）=-2．当a≥0时，f（a）=-a2=-2；当a＜0时，f（a）=a2+2a+2=-2．由此能求出a的值．
解答 解：∵f（x）=$\left\{{\begin{array}{l}{{x^2}+2x+2（x＜0）}\\{-{x^2}（x≥0）}\end{array}}\right.$，f（f（a））=2，
∴当f（a）≥0时，f（f（a））=-[f（a）]2=2，不成立；
当f（a）＜0时，f（f（a））=（f（a））2+2f（a）+2=2，
解得f（a）=0（舍），或f（a）=-2，
故f（a）=-2，
当a≥0时，f（a）=-a2=-2，解得a=$\sqrt{2}$或a=-$\sqrt{2}$（舍），
当a＜0时，f（a）=a2+2a+2=-2，无解．
综上，a=$\sqrt{2}$．
故答案为：$\sqrt{2}$．
点评 本题考查函数值的求法，是基础题，解题时要认真审题，注意函数性质的合理运用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
20．三棱锥SABC及其三视图中的正视图和侧视图如图所示，则棱SB的长为（ ）
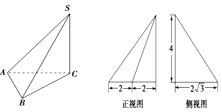
| A． | 4$\sqrt{2}$ | B． | $\sqrt{19}$ | C． | $\sqrt{20}$ | D． | $4\sqrt{3}$ |
7．在物理实验中，为了研究所挂物体的重量x对弹簧长度y的影响．某学生通过实验测量得到物体的重量与弹簧长度的对比表：
（1）利用最小二乘法求y对x的回归直线方程；
（2）预测所挂物体重量为8g时的弹簧长度．
（参考公式及数据：$b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x•\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{\overline x}^2}}}，a=\overline y-b\overline x$，$\sum_{i=1}^5{{x_i}^2}=55$$\sum_{i=1}^5{{x_i}{y_i}}=72$）
| 物体重量（单位g） | 1 | 2 | 3 | 4 | 5 |
| 弹簧长度（单位cm） | 1.5 | 3 | 4 | 5 | 6.5 |
（2）预测所挂物体重量为8g时的弹簧长度．
（参考公式及数据：$b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x•\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{\overline x}^2}}}，a=\overline y-b\overline x$，$\sum_{i=1}^5{{x_i}^2}=55$$\sum_{i=1}^5{{x_i}{y_i}}=72$）
4．在棱锥P-ABC中，侧棱PA、PB、PC两两垂直，Q为底面△ABC内一点，若点Q到三个侧面的距离分别为3、4、5，则以线段PQ为直径的球的体积为（ ）
| A． | $\frac{125π}{6}$ | B． | $\frac{{125\sqrt{2}π}}{3}$ | C． | $\frac{50π}{3}$ | D． | $\frac{25π}{3}$ |
18．集合M={x|x2-x-6≥0}，集合N={x|-3≤x≤1}，则N∩（∁RM）等于（ ）
| A． | [-2，1] | B． | （-2，1] | C． | [-3，3） | D． | （-2，3） |