题目内容
12．不等式|1-3x|≤2的解集为（ ）| A． | （-∞，-1] | B． | [-$\frac{1}{3}$，+∞） | C． | [-$\frac{1}{3}$，1] | D． | [-1，$\frac{1}{3}$] |
分析 不等式即-2≤3x-1≤2，由此求得x的范围．
解答 解：|1-3x|≤2，即-2≤3x-1≤2，求得-$\frac{1}{3}$≤x≤1，
故选：C．
点评 本题主要考查绝对值不等式的解法，体现了转化的数学思想，属于基础题．
练习册系列答案
相关题目
5．
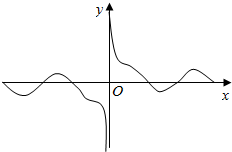如图是函数Q（x）的图象的一部分，设函数f（x）=sinx，g（x）=$\frac{1}{x}$，则Q（x）是（ ）
如图是函数Q（x）的图象的一部分，设函数f（x）=sinx，g（x）=$\frac{1}{x}$，则Q（x）是（ ）| A． | $\frac{f（x）}{g（x）}$ | B． | f （x）g （x） | C． | f （x）-g（x） | D． | f（x）+g（x） |
6．已知f（x+1）的定义域为（-1，2），则函数y=f（2x-1）的定义域为（ ）
| A． | $（{\frac{1}{2}，2}）$ | B． | （-1，2） | C． | $[{\frac{1}{2}，2}]$ | D． | [-1，2] |