题目内容
已知当x＞0时，函数f（x）=（2a-1）x（{a＞0，且a≠
）的值总大于1，则函数y=a2x-x2的单调增区间是 ．
| 1 |
| 2 |
考点：复合函数的单调性
专题：函数的性质及应用
分析：根据指数函数的性质结合复合函数单调性之间的关系即可得到结论．
解答：
解：当x＞0时，函数f（x）=（2a-1）x（{a＞0，且a≠
）的值总大于1，
即2a-1＞1，解得a＞1，
设t=2x-x2，则函数y=ax为增函数，
则要求函数y=a2x-x2的单调增区间，
即求t=2x-x2，的增区间，
∵函数t=2x-x2的增区间为（-∞，1），
∴函数y=a2x-x2的单调增区间是（-∞，1），
故答案为：（-∞，1）（或（-∞，1]）
| 1 |
| 2 |
即2a-1＞1，解得a＞1，
设t=2x-x2，则函数y=ax为增函数，
则要求函数y=a2x-x2的单调增区间，
即求t=2x-x2，的增区间，
∵函数t=2x-x2的增区间为（-∞，1），
∴函数y=a2x-x2的单调增区间是（-∞，1），
故答案为：（-∞，1）（或（-∞，1]）
点评：本题主要考查单调区间的求解，根据指数函数单调以及复合函数单调性之间的关系是解决本题的关键．
练习册系列答案
相关题目
已知y=f （x）是奇函数，当x∈（0，1）时，f（x）=lg
，那么当x∈（-1，0）时，f（x）的
表达式是（ ）
| 1 |
| 1-x |
表达式是（ ）
| A、f（x）=-lg（1-x） |
| B、f（x）=-lg（1+x） |
| C、f（x）=lg（1-x） |
| D、f（x）=lg（1+x） |
下列函数中满足“定义域的任意x都有f（-x）=f（x），且当0＜x1＜x2，都有f（x1）＜f（x2）”的是（ ）
A、y=
| ||
| B、y=e-x | ||
| C、y=-x2+1 | ||
| D、y=lg|x| |
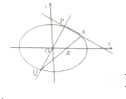如图，已知y=kx（k≠0）与椭圆：