题目内容
19.已知α,β∈(0,$\frac{π}{2}$),cosα=$\frac{1}{7}$,cos(α+β)=-$\frac{11}{14}$,则角β=( )| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{5π}{12}$ | D. | $\frac{π}{4}$ |
分析 由题意求出α+β的范围,由条件和平方关系分别求出sinα、sin(α+β),由角之间的关系和两角差的余弦函数求出cosβ,由β的范围和特殊角的三角函数值求出β.
解答 解:∵α,β∈(0,$\frac{π}{2}$),∴α+β∈(0,π),
∵cosα=$\frac{1}{7}$,∴sinα=$\sqrt{1-co{s}^{2}α}$=$\frac{4\sqrt{3}}{7}$,
∵cos(α+β)=-$\frac{11}{14}$,
∴sin(α+β)=$\sqrt{1-co{s}^{2}(α+β)}$=$\frac{5\sqrt{3}}{14}$,
∴cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα
=$\frac{1}{7}×(-\frac{11}{14})+\frac{5\sqrt{3}}{14}×\frac{4\sqrt{3}}{7}$=$\frac{1}{2}$
∴β=$\frac{π}{3}$,
故选A.
点评 本题考查两角差的余弦函数,平方关系,以及变角在三角函数求值中的应用,注意角的范围,考查化简、计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
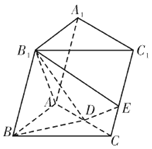 如图,在三棱柱ABC-A1B1C1中,B1B=B1A=AB=BC,∠B1BC=90°,D为AC的中点,AB⊥B1D.
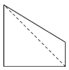
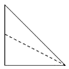
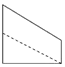
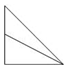
如图,在三棱柱ABC-A1B1C1中,B1B=B1A=AB=BC,∠B1BC=90°,D为AC的中点,AB⊥B1D.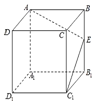 如图,点E为正方体ABCD-A1B1C1D1的棱BB1的中点,用过点A,E,C1的平面截去该正方体的上半部分,则剩余几何体的侧视图为( )
如图,点E为正方体ABCD-A1B1C1D1的棱BB1的中点,用过点A,E,C1的平面截去该正方体的上半部分,则剩余几何体的侧视图为( )