题目内容
在△ABC中，已知边c=10，又知
，求边a、b 的长．
解：∵=
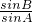
∴sinA•cosA=sinB•cosB
即sin2A=sin2B
由
∴a≠b，故A≠B
∴2A+2B=π
即A+B=
，
∴C=，
又∵c=10，
∴a=6，b=8，
所求a，b的长为：6，8．
分析：由，结合正弦定理，易判断三角形的形状，进而给出三角形的三边长，即可得到结论．
点评：本题考查的知识有正弦定理，根据三角形形状，求出三角形的边长，考查计算能力．
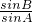
=∴sinA•cosA=sinB•cosB
即sin2A=sin2B
由
∴a≠b，故A≠B∴2A+2B=π
即A+B=
，∴C=
，又∵c=10，
∴a=6，b=8，
所求a，b的长为：6，8．
分析：由
，结合正弦定理，易判断三角形的形状，进而给出三角形的三边长，即可得到结论．点评：本题考查的知识有正弦定理，根据三角形形状，求出三角形的边长，考查计算能力．
练习册系列答案
名校课堂系列答案
相关题目