题目内容
12．在数列{an}中，a1=1，a1+$\frac{{a}_{2}}{{2}^{2}}$+$\frac{{a}_{3}}{{3}^{2}}$+…+$\frac{{a}_{n}}{{n}^{2}}$=an（n∈N*），则数列{an}的通项公式an=$\frac{2n}{n+1}$．分析 a1=1，a1+$\frac{{a}_{2}}{{2}^{2}}$+$\frac{{a}_{3}}{{3}^{2}}$+…+$\frac{{a}_{n}}{{n}^{2}}$=an（n∈N*），n≥2时，a1+$\frac{{a}_{2}}{{2}^{2}}$+$\frac{{a}_{3}}{{3}^{2}}$+…+$\frac{{a}_{n-1}}{（n-1）^{2}}$=an-1．相减可得：$\frac{n+1}{n}{a}_{n}$=$\frac{n}{n-1}{a}_{n-1}$．再利用递推关系即可得出．
解答 解：∵a1=1，a1+$\frac{{a}_{2}}{{2}^{2}}$+$\frac{{a}_{3}}{{3}^{2}}$+…+$\frac{{a}_{n}}{{n}^{2}}$=an（n∈N*），
n≥2时，a1+$\frac{{a}_{2}}{{2}^{2}}$+$\frac{{a}_{3}}{{3}^{2}}$+…+$\frac{{a}_{n-1}}{（n-1）^{2}}$=an-1．
∴$\frac{{a}_{n}}{{n}^{2}}$=an-an-1，
化为：$\frac{n+1}{n}{a}_{n}$=$\frac{n}{n-1}{a}_{n-1}$．
∴$\frac{n+1}{n}{a}_{n}$=…=2a1=2．
∴an=$\frac{2n}{n+1}$．
故答案为：$\frac{2n}{n+1}$．
点评 本题考查了数列递推关系、通项公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
20．已知$α∈（0，\frac{π}{6}）$，$sin（α+\frac{π}{3}）=\frac{12}{13}$，则$cos（\frac{π}{6}-α）$=（ ）
| A． | $\frac{5}{12}$ | B． | $\frac{12}{13}$ | C． | $-\frac{5}{13}$ | D． | $-\frac{12}{13}$ |
17．函数f（x）=asinωx+acosωx（a＞0，ω＞0）的图象如图所示，则实数a和ω的最小正值分别为（ ）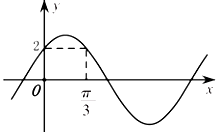
| A． | a=2，ω=2 | B． | a=2，ω=1 | C． | a=2，$ω=\frac{3}{2}$ | D． | a=2，$ω=\frac{1}{2}$ |
4．
持续性的雾霾天气严重威胁着人们的身体健康，汽车排放的尾气是造成雾霾天气的重要因素之一．为了贯彻落实国务院关于培育战略性新兴产业和加强节能减排工作的部署和要求，中央财政安排专项资金支持开展私人购买新能源汽车补贴试点．2017年国家又出台了调整新能源汽车推广应用财政补贴的新政策，其中新能源乘用车推广应用补贴标准如表：
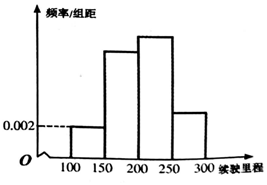
某课题组从汽车市场上随机选取了20辆纯电动乘用车，根据其续驶里程R（单词充电后能行驶的最大里程，R∈[100，300]）进行如下分组：第1组[100，150），第2组[150，200），第3组[200，250），第4组[250，300]，制成如图所示的频率分布直方图．已知第1组与第3组的频率之比为1：4，第2组的频数为7．
（1）请根据频率分布直方图统计这20辆纯电动乘用车的平均续驶里程；
（2）若以频率作为概率，设ξ为购买一辆纯电动乘用车获得的补贴，求ξ的分布列和数学期望E（ξ）．
持续性的雾霾天气严重威胁着人们的身体健康，汽车排放的尾气是造成雾霾天气的重要因素之一．为了贯彻落实国务院关于培育战略性新兴产业和加强节能减排工作的部署和要求，中央财政安排专项资金支持开展私人购买新能源汽车补贴试点．2017年国家又出台了调整新能源汽车推广应用财政补贴的新政策，其中新能源乘用车推广应用补贴标准如表：某课题组从汽车市场上随机选取了20辆纯电动乘用车，根据其续驶里程R（单词充电后能行驶的最大里程，R∈[100，300]）进行如下分组：第1组[100，150），第2组[150，200），第3组[200，250），第4组[250，300]，制成如图所示的频率分布直方图．已知第1组与第3组的频率之比为1：4，第2组的频数为7．
| 纯电动续驶里程R（公里） | 100≤R＜150 | 150≤R＜250 | R＞250 |
| 补贴标准（万元/辆） | 2 | 3.6 | 44 |
（2）若以频率作为概率，设ξ为购买一辆纯电动乘用车获得的补贴，求ξ的分布列和数学期望E（ξ）．