题目内容
17.函数f(x)=asinωx+acosωx(a>0,ω>0)的图象如图所示,则实数a和ω的最小正值分别为( )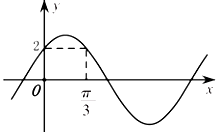
| A. | a=2,ω=2 | B. | a=2,ω=1 | C. | a=2,$ω=\frac{3}{2}$ | D. | a=2,$ω=\frac{1}{2}$ |
分析 利用两角和的正弦函数公式化简函数解析式可得f(x)=$\sqrt{2}$asin(ωx+$\frac{π}{4}$),由于点($\frac{π}{3}$,2),(0,2)在函数图象上,可求a,sin($\frac{π}{3}$ω+$\frac{π}{4}$)=$\frac{\sqrt{2}}{2}$,进而结合ω>0,可得ω的最小正值.
解答 解:∵f(x)=asinωx+acosωx=$\sqrt{2}$asin(ωx+$\frac{π}{4}$),
由于点($\frac{π}{3}$,2),(0,2)在函数图象上,
可得:2=$\sqrt{2}$asin($\frac{π}{3}$ω+$\frac{π}{4}$),且2=$\sqrt{2}$asin$\frac{π}{4}$,
解得:a=2,sin($\frac{π}{3}$ω+$\frac{π}{4}$)=$\frac{\sqrt{2}}{2}$,
可得:$\frac{π}{3}$ω+$\frac{π}{4}$=2kπ+$\frac{π}{4}$,k∈Z,或$\frac{π}{3}$ω+$\frac{π}{4}$=2kπ+$\frac{3π}{4}$,k∈Z,解得:ω=6k,k∈Z,或ω=6k+$\frac{3}{2}$,k∈Z,
由于ω>0,可得,ω的最小正值为$\frac{3}{2}$.
故选:C.
点评 本题主要考查了两角和的正弦函数公式,正弦函数的图象和性质的综合应用,考查了转化思想和数形结合思想,属于基础题.

练习册系列答案
相关题目
7.命题p:关于x的方程x2+ax+2=0无实根,命题q:函数f(x)=logax在(0,+∞)上单调递增,若“p∧q”为假命题,“p∨q”真命题,则实数a的取值范围是( )
| A. | (-2$\sqrt{2}$,+∞) | B. | (-2$\sqrt{2}$,2$\sqrt{2}$) | C. | (-2$\sqrt{2}$,1]∪[2$\sqrt{2}$,+∞) | D. | (-∞,2$\sqrt{2}$) |
2.已知函数f(x)=(2017x-$\frac{1}{201{7}^{x}}$)x2017,若f(log2a)+f(log0.5a)≤$\frac{2(201{7}^{2}-1)}{2017}$,则实数a的取值范围是( )
| A. | (0,2] | B. | (0,$\frac{2}{3}$]∪[1,+∞) | C. | (0,$\frac{1}{2}$]∪[2,+∞) | D. | [$\frac{1}{2}$,2] |
9.四棱锥P-ABCD的底面ABCD为正方形,PA⊥底面ABCD,若AB=2,PA=1,则此四棱锥的外接球的体积为( )
| A. | 36π | B. | 16π | C. | $\frac{9π}{2}$ | D. | $\frac{9π}{4}$ |