题目内容
(本小题满分13分).某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为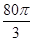 立方米,且
立方米,且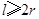 .假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为
.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为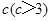 千元,设该容器的建造费用为
千元,设该容器的建造费用为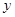 千元.
千元.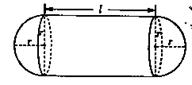
(Ⅰ)写出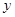 关于
关于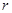 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域;
(Ⅱ)求该容器的建造费用最小时的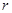 .
.
(I)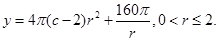 ;
;
(II) 是函数y的极小值点,也是最小值点。
是函数y的极小值点,也是最小值点。
(2)当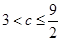 时,建造费用最小时
时,建造费用最小时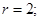 当
当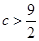 时,建造费用最小时
时,建造费用最小时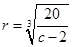 。
。
解析试题分析:(I)设容器的容积为V,
由题意知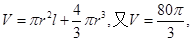
故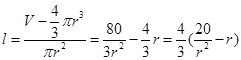
由于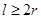
因此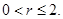 …………………………………………………………………….3分
…………………………………………………………………….3分
所以建造费用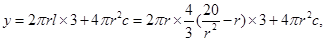
因此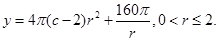 ………………………………………..5分
………………………………………..5分
(II)由(I)得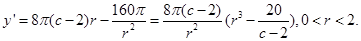
由于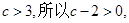
当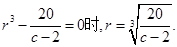
令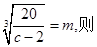
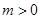
所以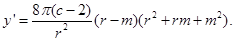 ………………………………….7分
………………………………….7分
(1)当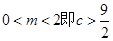 时,
时,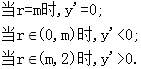
所以 是函数y的极小值点,也是最小值点。………………….10分
是函数y的极小值点,也是最小值点。………………….10分
(2)当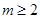 即
即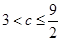 时,
时,
当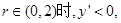 函数单调递减,
函数单调递减,
所以r=2是函数y的最小值点,
综上所述,当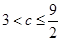 时,建造费用最小时
时,建造费用最小时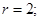
当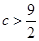 时,建造费用最小时
时,建造费用最小时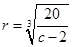 ………………13分
………………13分
考点:本题主要考查导数在实际问题中的应用,利用导数求函数的最值,几何体特征及体积计算。
点评:高考题,构建函数关系、准确求导数是解题的关键。

练习册系列答案
相关题目
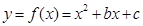 的图象过点(1,13),图像关于直线
的图象过点(1,13),图像关于直线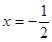 对称。
对称。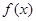 的解析式。
的解析式。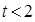 ,
,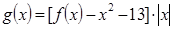 ,
,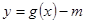 的零点有三个,求实数
的零点有三个,求实数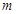 的取值范围;
的取值范围;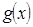 在[
在[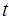 ,2]上的最小值。
,2]上的最小值。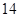 分)
分) 在定义域
在定义域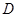 内某区间
内某区间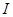 上是增函数,而
上是增函数,而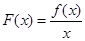 在
在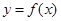 在
在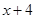 ,
,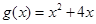 在
在 是否是“弱增函数”,
是否是“弱增函数”,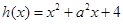 (
( 是常数且
是常数且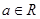 )在
)在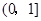 上是“弱增函数”.
上是“弱增函数”.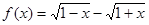 。
。 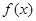 的定义域;
的定义域;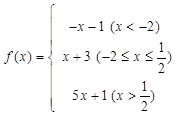 (
(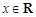 ),
),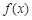 的最小值;
的最小值;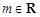 ,
,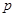 :关于
:关于 的不等式
的不等式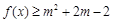 对任意
对任意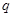 :函数
:函数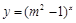 是增函数.若“
是增函数.若“ 的取值范围.
的取值范围.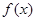 是定义在
是定义在 上的奇函数,当
上的奇函数,当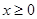 时,
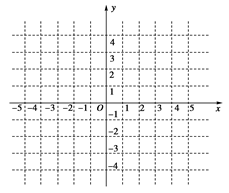
时,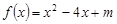 。
。
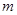 及
及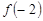 的值;
的值;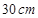 的
的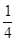 圆形(
圆形( 为圆心)铝皮上截取一块矩形材料
为圆心)铝皮上截取一块矩形材料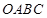 ,其中点
,其中点 在圆上,点
在圆上,点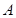 、
、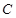 在两半径上,现将此矩形铝皮
在两半径上,现将此矩形铝皮 为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长
为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长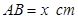 ,圆柱的体积为
,圆柱的体积为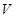
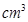 .
.
 的函数关系式,并指出定义域;
的函数关系式,并指出定义域; 上的函数
上的函数 ,如果满足:对任意
,如果满足:对任意 ,存在常数
,存在常数 ,都有
,都有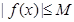 成立,则称
成立,则称 称为函数
称为函数 是否是有界函数,请写出详细判断过程;
是否是有界函数,请写出详细判断过程; ,若
,若 在
在 为上界,
为上界, 在
在 为上界;
为上界; 在
在 上是以3为上界的有界函数,
上是以3为上界的有界函数, 的取值范围.
的取值范围. 米.
米.