题目内容
(本小题满分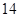 分)
分)
若函数 在定义域
在定义域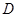 内某区间
内某区间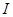 上是增函数,而
上是增函数,而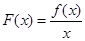 在
在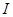 上是减函数,
上是减函数,
则称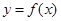 在
在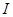 上是“弱增函数”
上是“弱增函数”
(1)请分别判断 =
=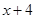 ,
,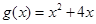 在
在 是否是“弱增函数”,
是否是“弱增函数”,
并简要说明理由;
(2)证明函数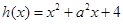 (
( 是常数且
是常数且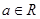 )在
)在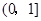 上是“弱增函数”.
上是“弱增函数”.
(1) =
=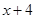 在
在 上是“弱增函数”;
上是“弱增函数”; 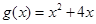 在
在 上不是“弱增函数”(2)易证
上不是“弱增函数”(2)易证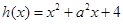 在
在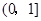 上是增函数,再利用定义证明
上是增函数,再利用定义证明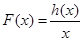 在
在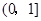 上是减函数
上是减函数
解析试题分析:(1) =
=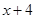 在
在 上是“弱增函数”;
上是“弱增函数”;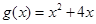 在
在 上不是“弱增函数”; ……2分
上不是“弱增函数”; ……2分
理由如下:
显然, =
=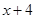 在
在 上是增函数,
上是增函数,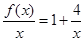 在
在 上是减函数,
上是减函数,
∴ =
=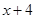 在
在 上是“弱增函数”。 ……4分
上是“弱增函数”。 ……4分
∵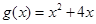 是开口向上的抛物线,对称轴方程为
是开口向上的抛物线,对称轴方程为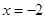 ,
,
∴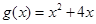 在
在 上是增函数,
上是增函数,
而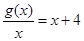 在
在 上是增函数,
上是增函数,
∴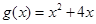 在
在 上不是“弱增函数”。 ……6分
上不是“弱增函数”。 ……6分
(2)证明:∵函数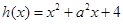 是开口向上的抛物线,对称轴方程为
是开口向上的抛物线,对称轴方程为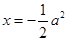 ,
,
∴函数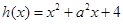 (
( 是常数且
是常数且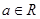 )在
)在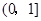 上是增函数; ……8分
上是增函数; ……8分
令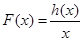 ,则
,则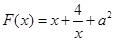 ,
,
对任意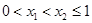 ,得
,得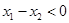 ,
,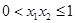 , ……9分
, ……9分
∵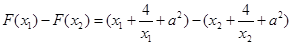
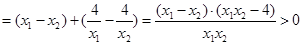 , ……12分
, ……12分
∴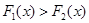 ,从而
,从而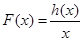 在
在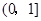 上是减函数, ……13分
上是减函数, ……13分
∴函数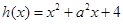 (
( 是常数且
是常数且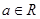 )在
)在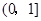 上是“弱增函数”. ……14分
上是“弱增函数”. ……14分
考点:本小题主要考查新定义下函数的单调性的研究和证明,考查学生的推理能力和论证能力.
点评:判断函数的单调性一是可以借助初等函数的单调性,再就是利用函数的单调性的定义来证明,利用定义证明函数的单调性时,要化到最简.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 ,且
,且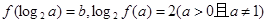 ,
,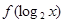 的最小值及相应 x的值;
的最小值及相应 x的值;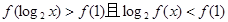 ,求x的取值范围.
,求x的取值范围.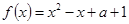
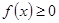 对一切实数
对一切实数 恒成立,求实数
恒成立,求实数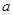 的取值范围.
的取值范围.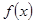 在区间
在区间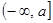 上的最小值
上的最小值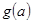 的表达式.
的表达式.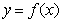 是定义在
是定义在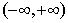 上的偶函数,当
上的偶函数,当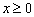 时,
时, 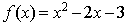 。
。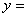
 在
在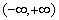 上的解析式;
上的解析式;  的大致图象;并根据图像写出
的大致图象;并根据图像写出 ;
;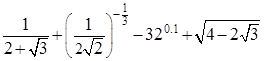 .
.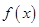 在定义域
在定义域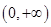 上为增函数,且满足
上为增函数,且满足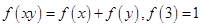
 的值 (2)解不等式
的值 (2)解不等式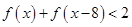
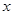 小时的收费为
小时的收费为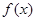 元
元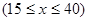 ,在乙家租一张球台开展活动
,在乙家租一张球台开展活动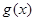 元
元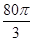 立方米,且
立方米,且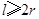 .假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为
.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为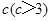 千元,设该容器的建造费用为
千元,设该容器的建造费用为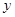 千元.
千元.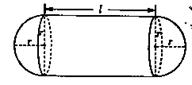
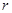 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域;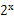 -2,若同时满足条件:
-2,若同时满足条件: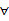 x∈R,f(x) <0或g(x) <0;②
x∈R,f(x) <0或g(x) <0;②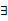 x∈(﹣∝, ﹣4),f(x)g(x) <0。求m的取值范围。
x∈(﹣∝, ﹣4),f(x)g(x) <0。求m的取值范围。