题目内容
12.椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为F1、F2,若椭圆上存在一点P使得∠F1PF2=90°,且|PF1|是|PF2|和|F1F2|的等差中项,则椭圆的离心率e为( )| A. | $\frac{5}{7}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{\sqrt{3}}{4}$ |
分析 设|PF1|=m,|PF2|=n,由题意可得:$\left\{\begin{array}{l}{m+n=2a}\\{2m=n+2c}\\{{m}^{2}+{n}^{2}=4{c}^{2}}\end{array}\right.$,化简即可得出.
解答 解:设|PF1|=m,|PF2|=n,
由题意可得:$\left\{\begin{array}{l}{m+n=2a}\\{2m=n+2c}\\{{m}^{2}+{n}^{2}=4{c}^{2}}\end{array}\right.$,化为:$(\frac{2a+2c}{3})^{2}$+$(\frac{4a-2c}{3})^{2}$=4c2,
∴7e2+2e-5=0,0<e<1.
解得e=$\frac{5}{7}$,
故选:A.
点评 本题考查了椭圆的标准方程及其性质、勾股定理、等差数列的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
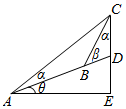 在斜度一定的山坡上的一点A测得山顶上一建筑物顶端C对于山坡的斜度为α,向山顶前进a米到达点B,从B点测得斜度为β,设建筑物的高为h米,山坡对于地平面的倾斜角为θ,则cosθ=$\frac{asinαsinβ}{hsin(β-α)}$.
在斜度一定的山坡上的一点A测得山顶上一建筑物顶端C对于山坡的斜度为α,向山顶前进a米到达点B,从B点测得斜度为β,设建筑物的高为h米,山坡对于地平面的倾斜角为θ,则cosθ=$\frac{asinαsinβ}{hsin(β-α)}$.