题目内容
15.已知函数f(x)=|2x-1|(Ⅰ)若不等式f(x+$\frac{1}{2}$)≤2m+1(m>0)的解集为[-$\frac{3}{2}$,$\frac{3}{2}$],求实数m的值;
(Ⅱ)若不等式f(x)≤|y|+|a-y|+|2x|,对任意的实数x,y∈R都成立,求正实数a的最小值.
分析 (Ⅰ)若不等式f(x+$\frac{1}{2}$)≤2m+1(m>0)的解集为[-$\frac{3}{2}$,$\frac{3}{2}$],不等式|2x|≤2m+1(m>0)的解集为[-$\frac{3}{2}$,$\frac{3}{2}$],解不等式,即可求实数m的值;
(Ⅱ)若不等式f(x)≤|y|+|a-y|+|2x|,对任意的实数x,y∈R都成立,则|2x-1|-|2x|≤|y|+|a-y|,利用(|2x-1|-|2x|)max=1,(|y|+|a-y|)min=a,即可得出结论.
解答 解:(Ⅰ)若不等式f(x+$\frac{1}{2}$)≤2m+1(m>0)的解集为[-$\frac{3}{2}$,$\frac{3}{2}$],
∴不等式|2x|≤2m+1(m>0)的解集为[-$\frac{3}{2}$,$\frac{3}{2}$],
由|2x|≤2m+1,可得-m-$\frac{1}{2}$≤x≤m+$\frac{1}{2}$,
∴m+$\frac{1}{2}$=$\frac{3}{2}$,∴m=1;
(Ⅱ)若不等式f(x)≤|y|+|a-y|+|2x|,对任意的实数x,y∈R都成立,则|2x-1|-|2x|≤|y|+|a-y|,
∵(|2x-1|-|2x|)max=1,(|y|+|a-y|)min=a,∴a≥1,
∴正实数a的最小值为1.
点评 本题考查不等式的解法,考查绝对值不等式的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
3.在平面直角坐标系中,直线y=$\sqrt{2}$x与圆O:x2+y2=1交于A、B两点.α、β的始边是x轴的非负半轴,终边分别在射线OA和OB上,则tan(α+β)的值为( )
| A. | -2$\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | 0 | D. | 2$\sqrt{2}$ |
7.集合$M=\left\{{\left.x\right|x=\frac{n}{2}+1,n∈Z}\right\}$,$N=\left\{{\left.y\right|y=m+\frac{1}{2},m∈Z}\right\}$,则两集合M,N的关系为( )
| A. | M∩N=∅ | B. | M=N | C. | M?N | D. | N?M |
5.关于函数f(x)=2cos2$\frac{x}{2}$+$\sqrt{3}$sinx(x∈[0,π])下列结论正确的是( )
| A. | 有最大值3,最小值-1 | B. | 有最大值2,最小值-2 | ||
| C. | 有最大值3,最小值0 | D. | 有最大值2,最小值0 |
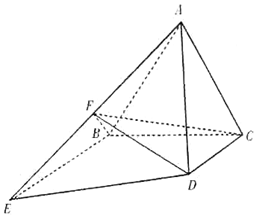 如图所示,正三角形ABC所在平面与梯形BCDE所在平面垂直,BE∥CD,BE=2CD=4,BE⊥BC,F为棱AB的中点.
如图所示,正三角形ABC所在平面与梯形BCDE所在平面垂直,BE∥CD,BE=2CD=4,BE⊥BC,F为棱AB的中点.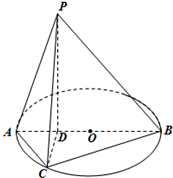 如图,已知PD垂直于以AB为直径的圆O所在的平面,点D在线段AB上,点C为圆O上一点,且BD=PD=3,AC=2AD=2.
如图,已知PD垂直于以AB为直径的圆O所在的平面,点D在线段AB上,点C为圆O上一点,且BD=PD=3,AC=2AD=2.