题目内容
(本小题满分12分)在四棱柱 中,
中, ,底面
,底面 为菱形,
为菱形,
 ,已知
,已知 .
.

(1)求证:平面 平面
平面 ;
;
(2)求点 到平面
到平面 的距离.
的距离.
【答案】(1)见解析;(2) .
.
【解析】
试题分析:(1)要证平面 平面
平面 ,即证
,即证 平面
平面 ,而
,而 可由菱形的性质得到,又由
可由菱形的性质得到,又由 底面
底面 ,得到
,得到 底面
底面 ,进而得到
,进而得到 ,从而使问题得证;(2)取
,从而使问题得证;(2)取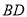 的中点
的中点 ,连接
,连接 ,
,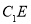 ,过
,过 作
作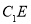 的垂线
的垂线 ,可知
,可知 为点
为点 到平面
到平面 的距离,从而通过解直角三角形求得
的距离,从而通过解直角三角形求得 的长.
的长.
试题解析:(1)依题意, 因为四棱柱 中,
中, 底面
底面 ,
,
所以 底面
底面 .
.
又 底面
底面 ,所以
,所以 .
.
因为 为菱形,所以
为菱形,所以 ,而
,而 ,所以
,所以 平面
平面 .
.
又 底面
底面 ,所以平面
,所以平面 平面
平面 .
.
(2)取 的中点
的中点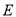 ,连接
,连接 ,
,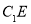 ,则
,则 ,
,

 ,故
,故
 ,
,
过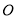 作
作 的垂线
的垂线 ,易证
,易证 ,即
,即 为点
为点 到平面
到平面 的距离.
的距离.
在直角三角形 中,
中, ,
, ,
, ,
,
所以 ,即点
,即点 到平面
到平面 的距离为
的距离为 .
.
考点:1、空间直线与平面的垂直的判定与性质;2、空间平面与平面垂直的判定;3、点到平面的距离.
【题型】解答题
【适用】一般
【标题】【百强校】2016届江西省临川一中高三上学期期中文科数学试卷(带解析)
【关键字标签】
【结束】
(本小题满分12分)已知函数 .
.
(1)当 时,求曲线
时,求曲线 在
在 处的切线方程;
处的切线方程;
(2)设函数 ,求函数
,求函数 的单调区间.
的单调区间.
练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目


 ,
, 为f (x)的导函数,令a=-
为f (x)的导函数,令a=- ,b=log32,则下列关系正确的是( )
,b=log32,则下列关系正确的是( ) 满足
满足 ,则
,则 的虚部为 ,
的虚部为 , .
. 的值是( )
的值是( ) 中,内角
中,内角 的对边分别为
的对边分别为 ,且
,且 .
. 的大小;
的大小; ,且
,且 的面积为
的面积为 ,求
,求 .
. (
( ).
). 的最大值;
的最大值; ,证明:
,证明: .
. 的边长为
的边长为 ,
, 、
、 分别为
分别为 、
、 的中点,沿
的中点,沿 ,
, ,
, 折成一个四面体,使
折成一个四面体,使 ,
, ,
, 三点重合,则这个四面体的体积为 .
三点重合,则这个四面体的体积为 . 上的函数
上的函数 满足下列两个条件:(1)对任意的
满足下列两个条件:(1)对任意的 恒有
恒有 成立;(2)当
成立;(2)当 时,
时, .记函数
.记函数
 ,若函数
,若函数 恰有两个零点,则实数
恰有两个零点,则实数 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
 的一元二次方程
的一元二次方程 的两个实数根分别是
的两个实数根分别是 ,且
,且 ,则
,则 的值是 ( )
的值是 ( )