题目内容
【题目】已知函数![]() .
.
(1)讨论![]() 在
在![]() 上极值点的个数;
上极值点的个数;
(2)若![]() 是函数
是函数![]() 的两个极值点,且
的两个极值点,且![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)当![]() 时,
时,![]() 在
在![]() 上无极值点;当
上无极值点;当![]() 时,
时,![]() 在
在![]() 上有两个极值点;当
上有两个极值点;当![]() 时,
时,![]() 在
在![]() 上只有一个极值点.;(2)
上只有一个极值点.;(2)![]() .
.
【解析】
(1)首先求导得到![]() ,分类讨论
,分类讨论![]() 的范围,求其单调区间,再根据单调区间即可得到极值点个数.
的范围,求其单调区间,再根据单调区间即可得到极值点个数.
(2)首先根据题意得到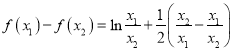 ,再令
,再令![]() ,构造函数
,构造函数![]() ,求出
,求出![]() 的最小值,即可得到实数
的最小值,即可得到实数![]() 的取值范围.
的取值范围.
(1)![]() ,令
,令![]() ,
,
所以![]() ,
,![]() ,
,
①当![]() ,即
,即![]() 时,
时,![]() 恒成立,
恒成立,
即![]() ,
,![]() 为增函数,此时
为增函数,此时![]() 在
在![]() 上无极值点;
上无极值点;
②当![]() ,即
,即![]() 时,由
时,由![]() 得,
得,![]() ,
,![]() .
.
(i)若![]() ,则
,则![]() ,
,
![]() .
.
则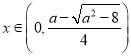 ,
,![]() ,
,![]() 为增函数,
为增函数,
 ,
,![]() ,
,![]() 为减函数,
为减函数,
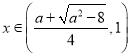 ,
,![]() ,
,![]() 为增函数,
为增函数,
故此时![]() 在
在![]() 上有两个极值点;
上有两个极值点;
(ii)若![]() ,则
,则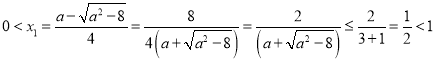 ,
,
而![]() .
.
则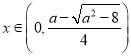 ,
,![]() ,
,![]() 为增函数,
为增函数,
 ,
,![]() ,
,![]() 为减函数,
为减函数,
故此时![]() 在
在![]() 上只有一个极值点;
上只有一个极值点;
综上可知,当![]() 时,
时,![]() 在
在![]() 上无极值点;
上无极值点;
当![]() 时,
时,![]() 在
在![]() 上有两个极值点;
上有两个极值点;
当![]() 时,
时,![]() 在
在![]() 上只有一个极值点.
上只有一个极值点.
(2)因为![]() 是函数
是函数![]() 的两个极值点,
的两个极值点,
所以令![]() ,得
,得![]() 是方程
是方程![]() 的两根,
的两根,
所以![]() ,即:
,即:![]() ,
,![]() ,
,![]() .
.
![]()
![]()
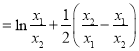
令![]() ,则
,则![]() ,
,![]() ,
,
又![]() ,
,
所以![]() 在区间
在区间![]() 内单调递减,
内单调递减,![]() ,即
,即![]() .
.
所以![]() ,即实数
,即实数![]() 的取值范围是
的取值范围是![]() .
.

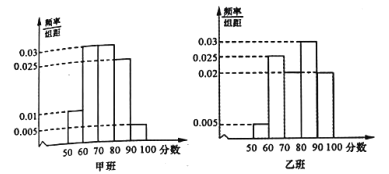
【题目】为了响应党的十九大所提出的教育教学改革,某校启动了数学教学方法的探索,学校将高一年级部分生源情况基本相同的学生分成甲、乙两个班,每班40人,甲班按原有传统模式教学,乙班实施自主学习模式.经过一年的教学实验,将甲、乙两个班学生一年来的数学成绩取平均数,两个班学生的平均成绩均在![]() ,按照区间
,按照区间![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 进行分组,绘制成如下频率分布直方图,规定不低于80分(百分制)为优秀.
进行分组,绘制成如下频率分布直方图,规定不低于80分(百分制)为优秀.
| 0.10 | 0.05 | 0.025 |
| 2.706 | 3.841 | 5.024 |
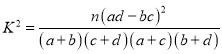
(1)完成表格,并判断是否有![]() 以上的把握认为“数学成绩优秀与教学改革有关”;
以上的把握认为“数学成绩优秀与教学改革有关”;
甲班 | 乙班 | 合计 | |
大于等于80分的人数 | |||
小于80分的人数 | |||
合计 |
(2)从乙班![]() ,
,![]() ,
,![]() 分数段中,按分层抽样随机抽取7名学生座谈,从中选三位同学发言,记来自
分数段中,按分层抽样随机抽取7名学生座谈,从中选三位同学发言,记来自![]() 发言的人数为随机变量
发言的人数为随机变量![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.