题目内容
2．已知集合M={a2，0}，N={1，a，2}，且M∩N={1}，那么M∪N的子集有16个．分析 由题意先确定集合M，N，再求M∪N={-1，0，1，2}，从而求子集的个数．
解答 解：∵M={a2，0}，N={1，a，2}，且M∩N={1}，
∴a=-1，
∴M∪N={-1，0，1，2}，
故M∪N的子集有24=16个．
故答案为：16．
点评 本题考查了集合的运算及集合的化简，同时考查了集合的子集个数问题，属于基础题．
练习册系列答案
七星图书口算速算天天练系列答案
初中学业考试导与练系列答案
相关题目
13．已知角α的终边过点P（-6，8），则cosα的值是（ ）
| A． | $-\frac{3}{5}$ | B． | $\frac{3}{5}$ | C． | $-\frac{4}{5}$ | D． | $\frac{4}{5}$ |
13．若存在两个正实数x，y，使得等式${x^3}{e^{\frac{y}{x}}}-a{y^3}=0$成立，其中e为自然对数的底数，则实数a的取值范围为（ ）
| A． | $[\frac{e^2}{8}，+∞）$ | B． | $（0，\frac{e^3}{27}]$ | C． | $[\frac{e^3}{27}，+∞）$ | D． | $（0，\frac{e^2}{8}]$ |
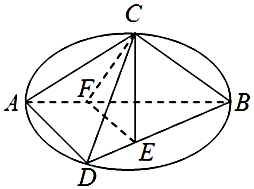如图C，D是以AB为直径的圆上的两点，AB=2AD=2$\sqrt{3}$，AC=BC，F是AB上的一点，且AF=$\frac{1}{3}$AB，CE⊥面ABD，CE=$\sqrt{2}$．
11．方程4x-2x-1+a=0有负根，则a的取值范围是（ ）
| A． | $a≥\frac{1}{8}$ | B． | $0＜a≤\frac{1}{16}$ | C． | $-\frac{1}{8}≤a＜0$ | D． | $-\frac{1}{2}＜a≤\frac{1}{16}$ |
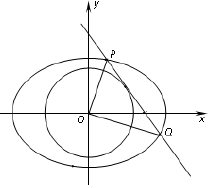如图，已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的离心率为$\frac{{\sqrt{2}}}{2}$，点（2，1）在椭圆C上．