题目内容
6.已知点P1(x1,y1)和P2(x2,y2),P是直线P1P2上一点,且P1P=-2PP2,则P点坐标为(-x1+2x2,-y1+2y2).分析 根据题意,设出点P的坐标,利用坐标表示出向量$\overrightarrow{{P}_{1}P}$与$\overrightarrow{{PP}_{2}}$,列出方程组求出点P的坐标.
解答 解:设P(x,y),则$\overrightarrow{{P}_{1}P}$=(x-x1,y-y1),$\overrightarrow{{PP}_{2}}$=(x2-x,y2-y);
又$\overrightarrow{{P}_{1}P}$=-2$\overrightarrow{{PP}_{2}}$,∴(x-x1,y-y1)=-2(x2-x,y2-y),
∴$\left\{\begin{array}{l}{x{-x}_{1}=-2{(x}_{2}-x)}\\{y{-y}_{1}=-2{(y}_{2}-y)}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x={-x}_{1}+{2x}_{2}}\\{y={-y}_{1}+{2y}_{2}}\end{array}\right.$,
∴点P的坐标为(-x1+2x2,-y1+2y2).
故答案为:(-x1+2x2,-y1+2y2).
点评 本题考查了平面向量的坐标表示与应用问题,也考查了方程组的解法与应用问题,是基础题目.

练习册系列答案
相关题目
16.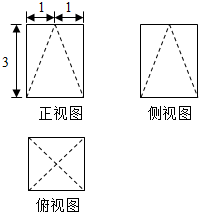 一个几何体的三视图如图所示,正视图与侧视图为全等的矩形,俯视图为正方形,则该几何体的体积为( )
一个几何体的三视图如图所示,正视图与侧视图为全等的矩形,俯视图为正方形,则该几何体的体积为( )
 一个几何体的三视图如图所示,正视图与侧视图为全等的矩形,俯视图为正方形,则该几何体的体积为( )
一个几何体的三视图如图所示,正视图与侧视图为全等的矩形,俯视图为正方形,则该几何体的体积为( )| A. | 8 | B. | 4 | C. | $\frac{8}{3}$ | D. | $\frac{4}{3}$ |
17.在三棱锥P-ABC中,PA⊥平面ABC,且AB⊥BC,AB=$\sqrt{6}$,PA=BC=$\sqrt{5}$,则三棱锥P-ABC的表面积为( )
| A. | 12π | B. | 16π | C. | 18π | D. | 24π |
1.Sn是数列{an}的前n项和log2Sn=n(n=1,2,3,…),那么数列{an}( )
| A. | 是公比为2的等比数列 | B. | 是公差为2的等差数列 | ||
| C. | 是公比为$\frac{1}{2}$的等比数列 | D. | 既非等差数列又非等比数列 |