题目内容
9.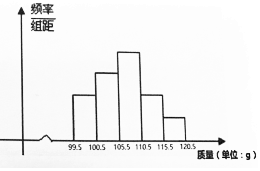 检测600个某产品的质量(单位:g),得到的直方图中,前三组的长方形的高度成等差数列,后三组对应的长方形的高度成公比为0.5的等比数列,已知检测的质量在100.5-105.5之间的产品数为150,则质量在115.5-120.5的长方形高度为( )
检测600个某产品的质量(单位:g),得到的直方图中,前三组的长方形的高度成等差数列,后三组对应的长方形的高度成公比为0.5的等比数列,已知检测的质量在100.5-105.5之间的产品数为150,则质量在115.5-120.5的长方形高度为( )| A. | $\frac{1}{12}$ | B. | $\frac{1}{30}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{60}$ |
分析 求出质量在100.5-105.5之间的频率,设出前三组长方形的高度成等差数列的公差为d,
利用频率和为1求出d的值,再求出115.5-120.5对应的长方形高.
解答 解:根据题意,质量在100.5-105.5之间的产品数为150,
频率为$\frac{150}{600}$=0.25;
前三组的长方形的高度成等差数列,设公差为d,
则根据频率和为1,得
(0.25-d)+0.25+(0.25+d)+$\frac{1}{2}$(0.25+d)+$\frac{1}{4}$(0.25+d)=1;
解得d=$\frac{1}{12}$;
所以质量在115.5-120.5的频率是
$\frac{1}{4}$×(0.25+$\frac{1}{12}$)=$\frac{1}{12}$,
对应小长方形的高为
$\frac{1}{12}$÷5=$\frac{1}{60}$.
故选:D.
点评 本题考查了频率分布直方图的应用问题,是基础题目.

练习册系列答案
相关题目
20.过点$P(2\sqrt{3},3)$且倾斜角为30o的直线方程为( )
| A. | .$y+4\sqrt{3}=3x$ | B. | .$y=x-\sqrt{3}$ | C. | $3y-3=\sqrt{3}x$ | D. | .$y-\sqrt{3}=\sqrt{3}x$ |
4.已知z=(m-3)+(m+1)i在复平面内对应的点在第二象限,则实数m的取值范围是( )
| A. | (-3,1) | B. | (-1,3) | C. | (1,+∞) | D. | (-∞,-3) |
18.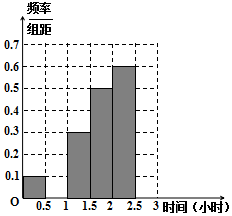 微信是现代生活进行信息交流的重要工具,随机对使用微信的60人进行了统计,得到如下数据统计表,每天使用微信时间在两小时以上的人被定义为“微信达人”,不超过两小时的人被定义为“非微信达人”.已知“非微信达人”与“微信达人”人数比恰为3:2.
微信是现代生活进行信息交流的重要工具,随机对使用微信的60人进行了统计,得到如下数据统计表,每天使用微信时间在两小时以上的人被定义为“微信达人”,不超过两小时的人被定义为“非微信达人”.已知“非微信达人”与“微信达人”人数比恰为3:2.
(Ⅰ)确定x,y,p,q的值,并补全频率分布直方图;
(Ⅱ)为进一步了解使用微信对自己的日常工作和生活是否有影响,从“非微信达人”和“微信达人”60人中用分层抽样的方法确定5人,若需从这5人中随机选取2人进行问卷调查,求选取的2人中恰有1人为“微信达人”的概率.
 微信是现代生活进行信息交流的重要工具,随机对使用微信的60人进行了统计,得到如下数据统计表,每天使用微信时间在两小时以上的人被定义为“微信达人”,不超过两小时的人被定义为“非微信达人”.已知“非微信达人”与“微信达人”人数比恰为3:2.
微信是现代生活进行信息交流的重要工具,随机对使用微信的60人进行了统计,得到如下数据统计表,每天使用微信时间在两小时以上的人被定义为“微信达人”,不超过两小时的人被定义为“非微信达人”.已知“非微信达人”与“微信达人”人数比恰为3:2.(Ⅰ)确定x,y,p,q的值,并补全频率分布直方图;
(Ⅱ)为进一步了解使用微信对自己的日常工作和生活是否有影响,从“非微信达人”和“微信达人”60人中用分层抽样的方法确定5人,若需从这5人中随机选取2人进行问卷调查,求选取的2人中恰有1人为“微信达人”的概率.
| 使用微信时间 (单位:小时) | 频数 | 频率 |
| (0,0.5] | 3 | 0.05 |
| (0.5,1] | x | p |
| (1,1.5] | 9 | 0.15 |
| (1.5,2] | 15 | 0.25 |
| (2,2.5] | 18 | 0.30 |
| (2.5,3] | y | q |
| 合计 | 60 | 1.00 |
19.执行如图所示的程序框图,则输出的s=( )


| A. | -1008 | B. | -1007 | C. | 1010 | D. | 1011 |
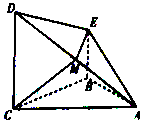 如图,在四棱锥A-BCDE中,CD⊥平面ABC,BE∥CD,AB=BC=CD,AB⊥BC,M为AD上一点,EM⊥平面ACD.
如图,在四棱锥A-BCDE中,CD⊥平面ABC,BE∥CD,AB=BC=CD,AB⊥BC,M为AD上一点,EM⊥平面ACD.