题目内容
设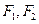 分别是椭圆
分别是椭圆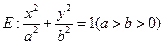 的左、右焦点,过
的左、右焦点,过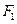 斜率为1的直线
斜率为1的直线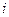 与
与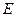 相交于
相交于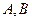 两点,且
两点,且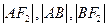 成等差数列。
成等差数列。
(1)求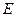 的离心率;
的离心率;
(2)设点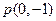 满足
满足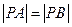 ,求
,求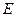 的方程
的方程
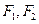 分别是椭圆
分别是椭圆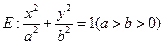 的左、右焦点,过
的左、右焦点,过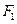 斜率为1的直线
斜率为1的直线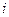 与
与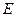 相交于
相交于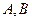 两点,且
两点,且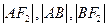 成等差数列。
成等差数列。(1)求
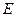 的离心率;
的离心率;(2)设点
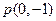 满足
满足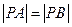 ,求
,求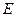 的方程
的方程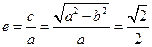 ,
,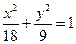
(I)由椭圆定义知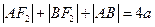 ,又
,又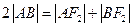 ,
,
得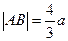
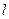 的方程为
的方程为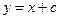 ,其中
,其中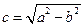 。
。
设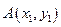 ,
,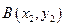 ,则A、B两点坐标满足方程组
,则A、B两点坐标满足方程组
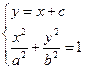
化简的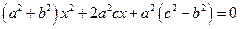
则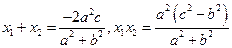
因为直线AB斜率为1,所以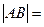
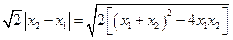
得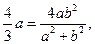 故
故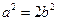
所以E的离心率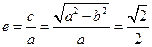
(II)设AB的中点为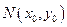 ,由(I)知
,由(I)知
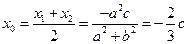 ,
,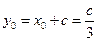 。
。
由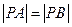 ,得
,得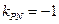 ,
,
即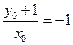
得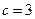 ,从而
,从而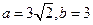
故椭圆E的方程为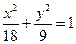 。
。
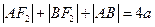 ,又
,又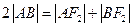 ,
,得
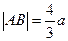
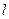 的方程为
的方程为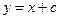 ,其中
,其中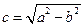 。
。设
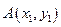 ,
,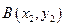 ,则A、B两点坐标满足方程组
,则A、B两点坐标满足方程组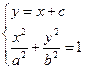
化简的
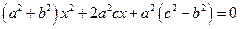
则
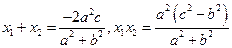
因为直线AB斜率为1,所以
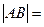
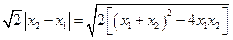
得
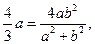 故
故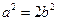
所以E的离心率
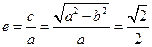
(II)设AB的中点为
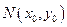 ,由(I)知
,由(I)知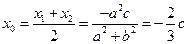 ,
,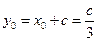 。
。由
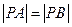 ,得
,得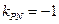 ,
,即
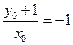
得
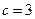 ,从而
,从而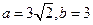
故椭圆E的方程为
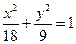 。
。
练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
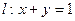 与椭圆
与椭圆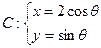 (
(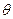 为参数),若直线
为参数),若直线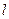 与椭圆交于A,B两点,求线段AB的长度。
与椭圆交于A,B两点,求线段AB的长度。
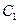 :
: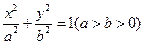 ,抛物线
,抛物线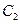 :
: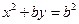 .
.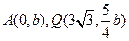 ,又
,又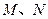 为
为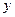 轴上的两个交点,若
轴上的两个交点,若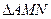 的垂心为
的垂心为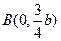 ,且
,且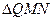 的重心在
的重心在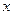 轴上的椭圆C的离心率为
轴上的椭圆C的离心率为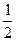 ,且经过点
,且经过点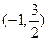 ,过点P(2,1)的直线
,过点P(2,1)的直线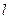 与椭圆C在第一象限相切于点M .
与椭圆C在第一象限相切于点M .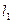 与椭圆C相交于不同的两点A、B,满足
与椭圆C相交于不同的两点A、B,满足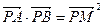 ?若存在,求出直线l1的方程;若不存在,请说明理由.
?若存在,求出直线l1的方程;若不存在,请说明理由.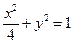 的焦点为点
的焦点为点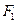 ,
,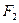 ,点
,点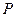 为椭圆上的一动点,当
为椭圆上的一动点,当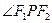 为钝角时,求点
为钝角时,求点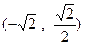 和B
和B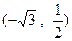 ,则椭圆的离心率为
,则椭圆的离心率为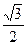
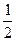
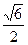
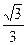
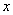 轴上,左右焦点分别为
轴上,左右焦点分别为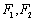 ,且
,且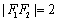 ,点(1,
,点(1,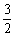 )在椭圆C上.
)在椭圆C上.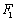 的直线
的直线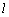 与椭圆
与椭圆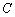 相交于
相交于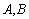 两点,且
两点,且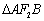 的面积为
的面积为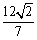 ,求以
,求以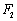 为圆心且与直线
为圆心且与直线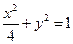 的焦点为
的焦点为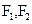 ,若点P在椭圆上,且满足
,若点P在椭圆上,且满足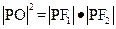 (其中
(其中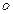 为坐标原点),则称点P为“★点”,那么下列结论正确的是 ( )
为坐标原点),则称点P为“★点”,那么下列结论正确的是 ( )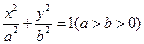 的右焦点且垂直于
的右焦点且垂直于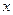 轴的直线与椭圆交于
轴的直线与椭圆交于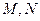 两点,以
两点,以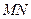 为直径的圆恰好过左焦点,则椭圆的离心率等于 。
为直径的圆恰好过左焦点,则椭圆的离心率等于 。