题目内容
已知中心在原点,焦点在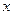 轴上的椭圆C的离心率为
轴上的椭圆C的离心率为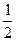 ,且经过点
,且经过点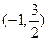 ,过点P(2,1)的直线
,过点P(2,1)的直线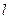 与椭圆C在第一象限相切于点M .
与椭圆C在第一象限相切于点M .
(1)求椭圆C的方程;
(2)求直线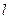 的方程以及点M的坐标;
的方程以及点M的坐标;
(3)是否存过点P的直线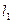 与椭圆C相交于不同的两点A、B,满足
与椭圆C相交于不同的两点A、B,满足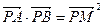 ?若存在,求出直线l1的方程;若不存在,请说明理由.
?若存在,求出直线l1的方程;若不存在,请说明理由.
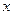 轴上的椭圆C的离心率为
轴上的椭圆C的离心率为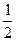 ,且经过点
,且经过点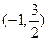 ,过点P(2,1)的直线
,过点P(2,1)的直线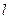 与椭圆C在第一象限相切于点M .
与椭圆C在第一象限相切于点M .(1)求椭圆C的方程;
(2)求直线
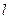 的方程以及点M的坐标;
的方程以及点M的坐标;(3)是否存过点P的直线
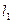 与椭圆C相交于不同的两点A、B,满足
与椭圆C相交于不同的两点A、B,满足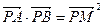 ?若存在,求出直线l1的方程;若不存在,请说明理由.
?若存在,求出直线l1的方程;若不存在,请说明理由.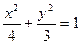 ,
,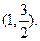 ,
,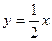
解(Ⅰ)设椭圆C的方程为 ,由题意得
,由题意得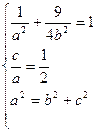
解得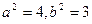 ,故椭圆C的方程为
,故椭圆C的方程为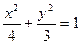 .……………………4分
.……………………4分
(Ⅱ)因为过点P(2,1)的直线l与椭圆在第一象限相切,所以l的斜率存在,故可调直线l的议程为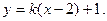
由 得
得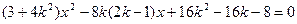 .①
.①
因为直线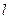 与椭圆相切,所以
与椭圆相切,所以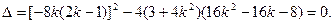
整理,得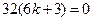 解得
解得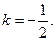
所以直线l方程为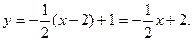
将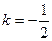 代入①式,可以解得M点横坐标为1,故切点M坐标为
代入①式,可以解得M点横坐标为1,故切点M坐标为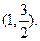 ……8分
……8分
(Ⅲ)若存在直线l1满足条件,的方程为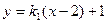 ,代入椭圆C的方程得
,代入椭圆C的方程得
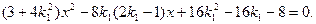
因为直线l1与椭圆C相交于不同的两点A,B,设A,B两点的坐标分别为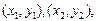
所以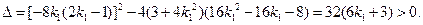
所以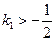 .
.
又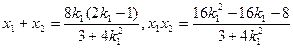 ,
,
因为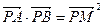 即
即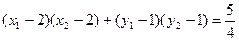 ,
,
所以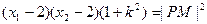
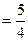 .
.
即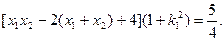
所以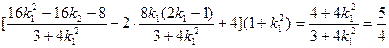 ,解得
,解得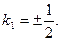 因为A,B为不同的两点,所以
因为A,B为不同的两点,所以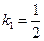 .
.
于是存在直线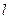 1满足条件,其方程为
1满足条件,其方程为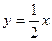 ………………………………12分
………………………………12分
 ,由题意得
,由题意得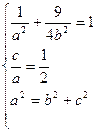
解得
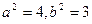 ,故椭圆C的方程为
,故椭圆C的方程为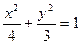 .……………………4分
.……………………4分(Ⅱ)因为过点P(2,1)的直线l与椭圆在第一象限相切,所以l的斜率存在,故可调直线l的议程为
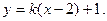
由
 得
得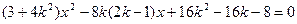 .①
.①因为直线
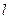 与椭圆相切,所以
与椭圆相切,所以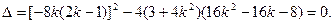
整理,得
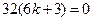 解得
解得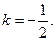
所以直线l方程为
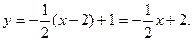
将
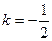 代入①式,可以解得M点横坐标为1,故切点M坐标为
代入①式,可以解得M点横坐标为1,故切点M坐标为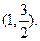 ……8分
……8分(Ⅲ)若存在直线l1满足条件,的方程为
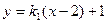 ,代入椭圆C的方程得
,代入椭圆C的方程得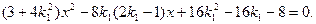
因为直线l1与椭圆C相交于不同的两点A,B,设A,B两点的坐标分别为
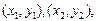
所以
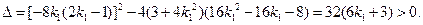
所以
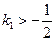 .
.又
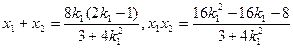 ,
,因为
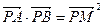 即
即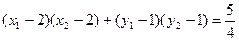 ,
,所以
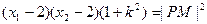
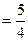 .
.即
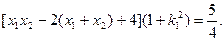
所以
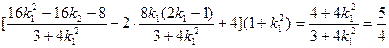 ,解得
,解得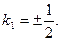 因为A,B为不同的两点,所以
因为A,B为不同的两点,所以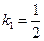 .
.于是存在直线
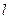 1满足条件,其方程为
1满足条件,其方程为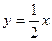 ………………………………12分
………………………………12分
练习册系列答案
相关题目
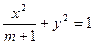 的两个焦点是
的两个焦点是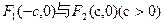 ,且椭圆上存在点M,使
,且椭圆上存在点M,使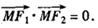
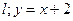 与椭圆存在一个公共点E,使得|EF
与椭圆存在一个公共点E,使得|EF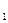 |+|EF
|+|EF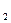 |取得最小值,求此最小值及此时椭圆的方程;
|取得最小值,求此最小值及此时椭圆的方程; 的直线
的直线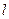 ,与椭圆交于不同的两A,B,满足
,与椭圆交于不同的两A,B,满足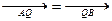 ,且使得过点
,且使得过点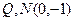 两点的直线NQ满足
两点的直线NQ满足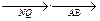 =0?若存在,求出k的取值范围;若不存在,说明理由
=0?若存在,求出k的取值范围;若不存在,说明理由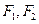 分别是椭圆
分别是椭圆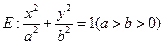 的左、右焦点,过
的左、右焦点,过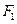 斜率为1的直线
斜率为1的直线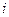 与
与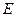 相交于
相交于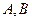 两点,且
两点,且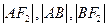 成等差数列。
成等差数列。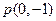 满足
满足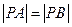 ,求
,求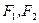 是椭圆
是椭圆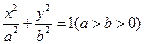 的两个焦点,
的两个焦点,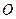 为坐标原点,点
为坐标原点,点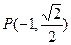 在椭圆上,且
在椭圆上,且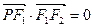 ,⊙
,⊙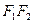 为直径的圆,直线
为直径的圆,直线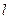 :
: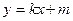 与⊙
与⊙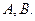
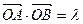 ,且满足
,且满足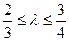 时,求弦长
时,求弦长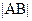 的取值范围.
的取值范围. :
: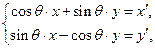 可把平面直角坐标系上的点
可把平面直角坐标系上的点 变换到这一平面上的点
变换到这一平面上的点 .特别地,若曲线
.特别地,若曲线 上一点
上一点 经变换公式
经变换公式 与点
与点 的中心为坐标原点,焦点在
的中心为坐标原点,焦点在 轴上,且焦距为
轴上,且焦距为 ,长轴顶点和短轴顶点间的距离为2. 求该椭圆
,长轴顶点和短轴顶点间的距离为2. 求该椭圆 时,其两个焦点
时,其两个焦点 、
、 经变换公式
经变换公式 和
和 的坐标;
的坐标; ,
,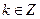 )下的不动点的存在情况和个数.
)下的不动点的存在情况和个数.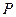 为椭圆
为椭圆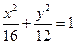 上任一点,当
上任一点,当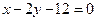 的距离的最小时,点
的距离的最小时,点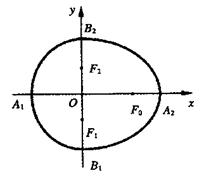
 合成的曲线称作“果圆”(其中
合成的曲线称作“果圆”(其中 )。如图,设点
)。如图,设点 是相应椭圆的焦点,A1、A2和B1、B2是“果圆”与x,y轴的交点,若△F0F1F2是边长为1的等边三角形,则a,b的值分别为 ( )
是相应椭圆的焦点,A1、A2和B1、B2是“果圆”与x,y轴的交点,若△F0F1F2是边长为1的等边三角形,则a,b的值分别为 ( )

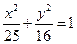 上,若F(3,0),
上,若F(3,0),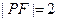 ,且M为PF中点,则
,且M为PF中点,则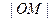 =_____.
=_____.