题目内容
4.设数列{an}的通项公式${a_n}=ncos\frac{nπ}{2}$,前n项和为Sn,则S2012=1006.分析 ${a_n}=ncos\frac{nπ}{2}$,可得n=2k-1(k∈N*),a2k-1=0.n=2k时,a2k=2kcoskπ=2k×(-1)k.即可得出.
解答 解:∵${a_n}=ncos\frac{nπ}{2}$,∴n=2k-1(k∈N*),a2k-1=0.
n=2k时,a2k=2kcoskπ=2k×(-1)k.
则S2012=a2+a4+…+a2012=-2+4-…+2012
=2×503=1006.
故答案为:1006.
点评 本题考查了数列通项公式、分组求和方法,考查了分类讨论方法、推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
14.函数y=$\sqrt{2x+1}$+$\sqrt{3-4x}$的定义域为( )
| A. | $(-\frac{1}{2},\frac{3}{4})$ | B. | $[{-\frac{1}{2},\frac{3}{4}}]$ | C. | $(-∞,\frac{1}{2}]$ | D. | $(-\frac{1}{2},0)∪(0,+∞)$ |
15.△ABC的内角A,B满足cosAcosB>sinAsinB,则△ABC是( )
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 等边三角形 |
19.函数y=ax,x∈[-1,2]的最大值与函数f(x)=x2-2x+3的最值相等,则a的值为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{2}$或2 | C. | $\frac{1}{2}$或2 | D. | $\frac{1}{2}或\sqrt{2}$ |
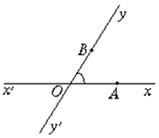 如图,有两条相交成60°角的直线xx′,yy′,交点是O,甲、乙分别在Ox,Oy上,起初甲离O点3km,乙离O点1km,后来两人同时用每小时4km的速度,甲沿xx′方向,乙沿y′y方向步行,问:
如图,有两条相交成60°角的直线xx′,yy′,交点是O,甲、乙分别在Ox,Oy上,起初甲离O点3km,乙离O点1km,后来两人同时用每小时4km的速度,甲沿xx′方向,乙沿y′y方向步行,问: 为贯彻落实教育部等6部门《关于加快发展青少年校园足球的实施意见》,全面提高我市中学生的体质健康水平,普及足球知识和技能,市教体局决定举行秋季校园足球联赛,为迎接此次联赛,甲中学选拔了20名学生组成集训队,现统计了这20名学生的身高,得到茎叶图如下:
为贯彻落实教育部等6部门《关于加快发展青少年校园足球的实施意见》,全面提高我市中学生的体质健康水平,普及足球知识和技能,市教体局决定举行秋季校园足球联赛,为迎接此次联赛,甲中学选拔了20名学生组成集训队,现统计了这20名学生的身高,得到茎叶图如下: