题目内容
2.(1)等比数列{an}中,已知a1+a2=324,a3+a4=36,求a5+a6.(2)已知数列{an}为等差数列,且a5=11,a8=5,求an.
分析 (1)由于{an}是等比数列,可得a1+a2,a3+a4,a5+a6也成等比数列,即可得出;
(2)利用等差数列的通项公式即可得出.
解答 解:(1)∵在等比数列{an}中,a1+a2,a3+a4,a5+a6也成等比数列,∵a1+a2=324,a3+a4=36,
∴${a_5}+{a_6}=\frac{36×36}{324}=4$.
(2)设公差为d,由a5=11,a8=5,
得$\left\{\begin{array}{l}{{a}_{1}+4d=11}\\{{a}_{1}+7d=5}\end{array}\right.$,解得$\left\{\begin{array}{l}{{a}_{1}=19}\\{d=-2}\end{array}\right.$.
∴an=19+(n-1)(-2)=-2n+21.
点评 本题考查了等差数列与等比数列的通项公式及其性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
14.已知{an}是公比小于1的等比数列,且a2=2,a1+a3=5,设Tn=a1a2+a2a3+a3a4+…+anan+1,则( )
| A. | 12≤Tn<16 | B. | 8≤Tn<16 | C. | 12≤Tn<$\frac{32}{3}$ | D. | 8≤Tn<$\frac{32}{3}$ |
11.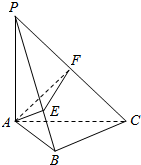 《九章算术》中,将四个面都为直角三角形的四面体称之为鳖臑,如图,在鳖臑PABC中,PA⊥平面ABC,AB⊥BC,且AP=AC=1,过A点分别作AE⊥PB于E、AF⊥PC于F,连接EF当△AEF的面积最大时,tan∠BPC的值是( )
《九章算术》中,将四个面都为直角三角形的四面体称之为鳖臑,如图,在鳖臑PABC中,PA⊥平面ABC,AB⊥BC,且AP=AC=1,过A点分别作AE⊥PB于E、AF⊥PC于F,连接EF当△AEF的面积最大时,tan∠BPC的值是( )
 《九章算术》中,将四个面都为直角三角形的四面体称之为鳖臑,如图,在鳖臑PABC中,PA⊥平面ABC,AB⊥BC,且AP=AC=1,过A点分别作AE⊥PB于E、AF⊥PC于F,连接EF当△AEF的面积最大时,tan∠BPC的值是( )
《九章算术》中,将四个面都为直角三角形的四面体称之为鳖臑,如图,在鳖臑PABC中,PA⊥平面ABC,AB⊥BC,且AP=AC=1,过A点分别作AE⊥PB于E、AF⊥PC于F,连接EF当△AEF的面积最大时,tan∠BPC的值是( )| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
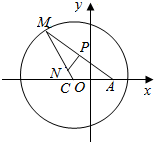 如图所示,已知圆(x+3)2+y2=100,定点A(3,0),M为圆C上一动点,点P在AM上,点N在CM上,且满足$\overrightarrow{AM}$=2$\overrightarrow{AP}$,$\overrightarrow{NP}$•$\overrightarrow{AM}$=0,点N的轨迹为曲线E.
如图所示,已知圆(x+3)2+y2=100,定点A(3,0),M为圆C上一动点,点P在AM上,点N在CM上,且满足$\overrightarrow{AM}$=2$\overrightarrow{AP}$,$\overrightarrow{NP}$•$\overrightarrow{AM}$=0,点N的轨迹为曲线E.