题目内容
10.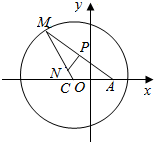 如图所示,已知圆(x+3)2+y2=100,定点A(3,0),M为圆C上一动点,点P在AM上,点N在CM上,且满足$\overrightarrow{AM}$=2$\overrightarrow{AP}$,$\overrightarrow{NP}$•$\overrightarrow{AM}$=0,点N的轨迹为曲线E.
如图所示,已知圆(x+3)2+y2=100,定点A(3,0),M为圆C上一动点,点P在AM上,点N在CM上,且满足$\overrightarrow{AM}$=2$\overrightarrow{AP}$,$\overrightarrow{NP}$•$\overrightarrow{AM}$=0,点N的轨迹为曲线E.(1)求曲线E的方程;
(2)求过点Q(2,1)的弦的中点的轨迹方程.
分析 (1)通过向量关系,判断点N的轨迹为曲线E.满足椭圆定义,然后求解椭圆的方程即可.
(2)利用点差法求斜率,即可求过点Q(2,1)的弦的中点的轨迹方程.
解答 解:(1)∵$\overrightarrow{AM}$=2$\overrightarrow{AP}$,$\overrightarrow{NP}$•$\overrightarrow{AM}$=0,
∴NP为AM的中垂线,
∴|NA|=|NM|.
又∵|CN|+|NM|=10,∴|CN|+|NA|=10>6,
∴动点N的轨迹是以点C和A为焦点的椭圆,且2a=10,
∴曲线E的方程为:$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{16}=1$;
(2)设直线与椭圆交与G(x1,y1)、H(x2,y2)两点,中点为S(x,y),
设弦的斜率k=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=-$\frac{16({x}_{1}+{x}_{2})}{25({y}_{1}+{y}_{2})}$=-$\frac{16x}{25y}$,
由S(x,y),Q(2,1)两点可得弦的斜率为k=$\frac{y-1}{x-2}$,
∴-$\frac{16x}{25y}$=$\frac{y-1}{x-2}$,化简可得中点的轨迹方程为:16x2+25y2-32x-25y=0.
点评 本题考查椭圆的定义的应用,轨迹方程的求法,考查计算能力.

练习册系列答案
相关题目
20.已知函数f(x)对任意x∈R都有f(x+2)=-f(x),且y=f(x-1)的图象关于点(1,0)对称,当x∈(0,2)时f(x)=2x2,则f(2015)=( )
| A. | -2 | B. | 2 | C. | -98 | D. | 98 |
18.a是f(x)=2x-log$\frac{1}{2}$x的零点,若k>a,则f(k)的值满足( )
| A. | f(k)=0 | B. | f(k)<0 | C. | f(k)>0 | D. | f(k)的符号不确定 |