Question

11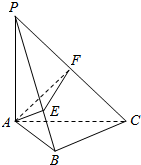．《九章算术》中，将四个面都为直角三角形的四面体称之为鳖臑，如图，在鳖臑PABC中，PA⊥平面ABC，AB⊥BC，且AP=AC=1，过A点分别作AE⊥PB于E、AF⊥PC于F，连接EF当△AEF的面积最大时，tan∠BPC的值是（　　）

• A． $\sqrt{2}$
• B． $\frac{\sqrt{2}}{2}$
• C． $\sqrt{3}$
• D． $\frac{\sqrt{3}}{3}$

Answer 1

分析 由已知可证AE⊥平面PBC，PC⊥平面AEF，可得△AEF、△PEF均为直角三角形，由已知得AF=$\frac{\sqrt{2}}{2}$，从而${S}_{△AEF}=\frac{1}{2}AE•EF≤\frac{1}{4}$（AE²+EF²）=$\frac{1}{4}$（AF）²=$\frac{1}{8}$，当且仅当AE=EF时，取“=”，
解得当AE=EF=$\frac{1}{2}$时，△AEF的面积最大，即可求得tan∠BPC=$\frac{EF}{PF}$的值．

解答 解：显然BC⊥平面PAB，则BC⊥AE，
又PB⊥AE，则AE⊥平面PBC，
于是AE⊥EF，且AE⊥PC，结合条件AF⊥PC得PC⊥平面AEF，
所以△AEF、△PEF均为直角三角形，由已知得AF=$\frac{\sqrt{2}}{2}$，
而${S}_{△AEF}=\frac{1}{2}AE•EF≤\frac{1}{4}$（AE²+EF²）=$\frac{1}{4}$（AF）²=$\frac{1}{8}$，当且仅当AE=EF时，取“=”，
所以，当AE=EF=$\frac{1}{2}$时，△AEF的面积最大，此时tan∠BPC=$\frac{EF}{PF}=\frac{\frac{1}{2}}{\frac{\sqrt{2}}{2}}$=$\frac{\sqrt{2}}{2}$，
故选：B．

点评 本题主要考查了直线与平面垂直的判定，不等式的解法及应用，同时考查了空间想象能力、计算能力和逻辑推理能力，属于中档题．