题目内容
17.已知圆锥的侧面展开图为一个圆心角为120°,且面积为3π的扇形,则该圆锥的体积等于$\frac{2\sqrt{2}}{3}π$.分析 设圆锥的母线为l,底面半径为r,由已知条件求出l=3,r=1,从而求出圆锥的高,由此能求出圆锥的体积.
解答 解:设圆锥的母线为l,底面半径为r,
∵3π=$\frac{1}{3}$πl2,∴l=3,
∴120°=$\frac{r}{3}$×360°,
∴r=1,
∴圆锥的高是$\sqrt{9-1}$=2$\sqrt{2}$,
∴圆锥的体积是$\frac{1}{3}$×π×12×2$\sqrt{2}$=$\frac{2\sqrt{2}}{3}π$.
故答案为:$\frac{2\sqrt{2}}{3}π$.
点评 本题考查圆锥的体积的求法,是中档题,解题时要认真审题,注意圆锥的性质的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.新高考政策已经在上海和浙江试验实施.为了解学生科目选择的意向,从某校高一学生中随机抽取30位同学,对其选课情况进行统计分析,得到频率分布表如下:
(Ⅰ)若所抽取的30位同学中,有2位同学选择了“历史、地理、生物”组合,3位同学选择了“物理、政治、历史”组合.求a、b、c的值;
(Ⅱ)在(Ⅰ)的条件下,将选择了“历史、地理、生物”组合的2位同学记为x1、x2,选择了“物理、政治、历史”组合的3位同学记为y1、y2、y3.现从这5位同学中任取2位(假定每位同学被抽中的可能性相同),写出所有可能的结果,并求这两位同学科目选择恰好相同的概率.
| 科目选择 | 物理 化学 生物 | 历史 地理 政治 | 物理 化学 地理 | 历史 地理 生物 | 物理 政治 历史 | 其他 |
| 频率 | $\frac{1}{5}$ | $\frac{1}{6}$ | $\frac{2}{15}$ | a | b | c |
(Ⅱ)在(Ⅰ)的条件下,将选择了“历史、地理、生物”组合的2位同学记为x1、x2,选择了“物理、政治、历史”组合的3位同学记为y1、y2、y3.现从这5位同学中任取2位(假定每位同学被抽中的可能性相同),写出所有可能的结果,并求这两位同学科目选择恰好相同的概率.
9.设集合A={x|-2≤x<2},集合B={x|-1<x<3},那么A∪B=( )
| A. | {x|-2≤x<3} | B. | {-1,0,1} | C. | {x|-1<x<2} | D. | {0,1,2} |
6.已知点M(x,y)满足$\left\{\begin{array}{l}x≥1\\ x-y+1≥0\\ 2x-y-2≤0\end{array}\right.$,若ax+y的最大值为1,则a的值为( )
| A. | -1 | B. | 1 | C. | 2 | D. | 3 |
16.中国历法推测遵循以测为辅、以算为主的原则.例如《周髀算经》和《易经》里对二十四节气的晷(guǐ)影长的记录中,冬至和夏至的晷影长是实测得到的,其它节气的晷影长则是按照等差数列的规律计算得出的.下表为《周髀算经》对二十四节气晷影长的记录,其中$115.1\frac{4}{6}$寸表示115寸$1\frac{4}{6}$分(1寸=10分).
已知《易经》中记录的冬至晷影长为130.0寸,夏至晷影长为14.8寸,那么《易经》中所记录的惊蛰的晷影长应为82寸.
| 节 气 | 冬至 | 小寒 (大雪) | 大寒 (小雪) | 立春 (立冬) | 雨水 (霜降) | 惊蛰 (寒露) | 春分 (秋分) | 清明 (白露) | 谷雨 (处暑) | 立夏 (立秋) | 小满 (大暑) | 芒种 (小暑) | 夏至 |
| 晷影 长 (寸) | 135.0 | $125.\frac{5}{6}$ | $115.1\frac{4}{6}$ | $105.2\frac{3}{6}$ | $95.3\frac{2}{6}$ | $85.4\frac{2}{6}$ | 75.5 | $66.5\frac{5}{6}$ | $55.6\frac{4}{6}$ | $45.7\frac{3}{6}$ | $35.8\frac{2}{6}$ | $25.9\frac{1}{6}$ | 16.0 |
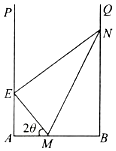 某地拟在一个U形水面PABQ(∠A=∠B=90°)上修一条堤坝(E在AP上,N在BQ上),围出一个封闭区域EABN,用以种植水生植物.为了美观起见,决定从AB上点M处分别向点E,N拉2条分割线ME,MN,将所围区域分成3个部分(如图),每部分种植不同的水生植物.已知AB=a,EM=BM,∠MEN=90°,设所拉分割线总长度为l.
某地拟在一个U形水面PABQ(∠A=∠B=90°)上修一条堤坝(E在AP上,N在BQ上),围出一个封闭区域EABN,用以种植水生植物.为了美观起见,决定从AB上点M处分别向点E,N拉2条分割线ME,MN,将所围区域分成3个部分(如图),每部分种植不同的水生植物.已知AB=a,EM=BM,∠MEN=90°,设所拉分割线总长度为l.