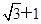题目内容
过双曲线 的左焦点
的左焦点 作圆
作圆 的切线,切点为
的切线,切点为 ,延长
,延长 交双曲线右支于点
交双曲线右支于点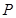 ,若
,若 ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A. | B.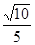 | C. | D. |
A
解析试题分析:∵|OF|=c,|OE|= ,∴|EF|=
,∴|EF|= ,∵
,∵ ,∴|PF|=2
,∴|PF|=2 ,
, =a,∵|PF|-
=a,∵|PF|- =2a,∴2
=2a,∴2 =3a,即
=3a,即 ,∴e=
,∴e= ,故选A.
,故选A.
考点:本题考查了双曲线离心率的求法
点评:通过几何关系构建关于a,b,c的起次方程是解决此类问题的关键

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
以双曲线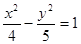 的离心率为首项,以函数
的离心率为首项,以函数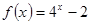 的零点为公比的等比数列的前
的零点为公比的等比数列的前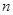 项的和
项的和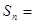
A.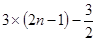 | B.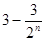 | C.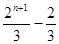 | D.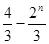 |
以双曲线 的离心率为半径,右焦点为圆心的圆与双曲线的渐近线相切,则
的离心率为半径,右焦点为圆心的圆与双曲线的渐近线相切,则 的值为( )
的值为( )
A. | B.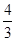 | C. | D.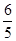 |
双曲线 =1的焦点到渐近线的距离为( )。
=1的焦点到渐近线的距离为( )。
A.2 | B.2 | C. | D.1 |
抛物线 上的点到直线
上的点到直线 距离的最小值是( )
距离的最小值是( )
A. | B. | C. | D. |
设抛物线 的焦点为
的焦点为 ,准线为
,准线为 ,
, 为抛物线上的一点,
为抛物线上的一点,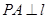 ,垂足为
,垂足为 .若直线
.若直线 的斜率为
的斜率为 ,则
,则
| A.4 | B.8 | C. | D. |
 ,虚轴的一个端点为
,虚轴的一个端点为 ,如果直线
,如果直线 与该双曲线的一条渐近线垂直,那么双曲线的离心率是 ( )
与该双曲线的一条渐近线垂直,那么双曲线的离心率是 ( )



 的准线方程是( )。
的准线方程是( )。 .
.
 .
.
 .
.
 .
.
 、
、 是椭圆
是椭圆 (a>b>0)的两个焦点,以线段
(a>b>0)的两个焦点,以线段