题目内容
6.若函数f(x)=$\frac{{2x}^{2}-a}{x-1}$(a<2)在区间(1,+∞)上的最小值为6,则实数a的值为( )| A. | 2 | B. | $\frac{3}{2}$ | C. | 1 | D. | $\frac{1}{2}$ |
分析 令t=x-1(t>0),即x=t+1,即有y=$\frac{2(t+1)^{2}-a}{t}$=2t+$\frac{2-a}{t}$+4(2<a),运用基本不等式可得最小值,再解方程即可得到所求a的值.
解答 解:令t=x-1(t>0),即x=t+1,
即有y=$\frac{2(t+1)^{2}-a}{t}$=2t+$\frac{2-a}{t}$+4(2<a),
≥2$\sqrt{2t•\frac{2-a}{t}}$+4=2$\sqrt{2(2-a)}$+4,
当且仅当2t=$\frac{2-a}{t}$时,取得最小值.
由题意可得2$\sqrt{2(2-a)}$+4=6,
解得a=$\frac{3}{2}$.
故选B.
点评 本题考查已知函数的最值求参数的值,注意运用换元法和基本不等式,注意满足的条件:一正二定三等,属于中档题.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
15.下列判断错误的是( )
| A. | “am2<bm2”是“a<b”的充分不必要条件 | |
| B. | 命题“?x∈R,x3-x2≤0”的否定是“?x∈R,x3-x2-1>0” | |
| C. | “若a=1,则直线x+y=0和直线x-ay=0互相垂直”的逆否命题为真命题 | |
| D. | 若p∧q为假命题,则p,q均为假命题 |
16.已知复数z,“z+$\overline{z}$=0”是“z为纯虚数”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分也不必要条件 |
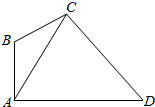 在如图所示的四边形ABCD中,已知AB⊥AD,∠ABC=120°,∠ACD=60°,AD=2$\sqrt{3}$,设∠ACB=θ,点C到AD的距离为h.
在如图所示的四边形ABCD中,已知AB⊥AD,∠ABC=120°,∠ACD=60°,AD=2$\sqrt{3}$,设∠ACB=θ,点C到AD的距离为h.