题目内容
下列函数中是偶函数的是（ ）
| A、y=x4（x＜0） | ||
| B、y=|x+1| | ||
C、y=
| ||
| D、y=3x-1 |
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：根据偶函数的定义进行判断即可得到结论．
解答：
解：A．函数的定义域关于原点不对称，为非奇非偶函数，
B．f（x）关于x=-1对称，对称轴不是y轴，不是偶函数，
C．函数f（x）的定义域为{x|x≠0}，则f（-x）=
+1=f（x），则f（x）为偶函数，
D．f（x）关于y轴不对称轴，不是偶函数．
故选：C
B．f（x）关于x=-1对称，对称轴不是y轴，不是偶函数，
C．函数f（x）的定义域为{x|x≠0}，则f（-x）=
| 2 |
| x2 |
D．f（x）关于y轴不对称轴，不是偶函数．
故选：C
点评：本题主要考查函数奇偶性的判断，根据函数的定义以及定义域的对称性是解决本题的关键．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
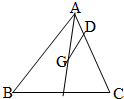
如图，正六边形ABCDEF的中心为O，若如图所示，在△ABC中，G为△ABC的重心，D在边AC上，且
=3
，则（ ）
| CD |
| DA |
A、
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、
|
已知sinθ=-
，θ∈（-
，0），则cos（θ-
）的值为（ ）
| 12 |
| 13 |
| π |
| 2 |
| π |
| 4 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
下列命题正确的是（ ）
| A、三角形的中位线平行且等于第三边 |
| B、对角线相等的四边形是等腰梯形 |
| C、四条边都相等的四边形是菱形 |
| D、相等的角是对顶角 |
已知不等式f（x）=
sin
cos
+cos2
-
-m≤0对于任意的-
≤x≤
恒成立，则实数m的取值范围是（ ）
| 3 |
| x |
| 4 |
| x |
| 4 |
| x |
| 4 |
| 1 |
| 2 |
| 5π |
| 6 |
| π |
| 6 |
A、m≥
| ||||||||
B、m≤
| ||||||||
C、m≤-
| ||||||||
D、-
|