题目内容
设数列 满足
满足

(1)求数列 的通项公式;
的通项公式;
(2)令 ,求数列
,求数列 的前n项和
的前n项和
(1)
(2)
解析试题分析:解、(1)当 时,
时,





 ,
,
当 时,
时, ,成立,
,成立,
所以通项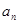

 5分
5分
(2)
 ,则
,则

令 ?,
?,
则 .?,
.?,
? ?得
?得

 -
-

所以 ,
,
则
 12分
12分
考点:错位相减法求和
点评:主要是考查了等比数列以及错位相减法求和 的运用,属于基础题。

练习册系列答案
相关题目
等比数列 中,
中, ,
, ,
, 分别是下表第一、二、三行中的某一个数,且
分别是下表第一、二、三行中的某一个数,且 ,
, ,
, 中的任何两个数不在下表的同一列.
中的任何两个数不在下表的同一列.
| | 第一列 | 第二列 | 第三列 |
| 第一行 | 3 | 2 | 10 |
| 第二行 | 6 | 4 | 14 |
| 第三行 | 9 | 8 | 18 |
 的通项公式;
的通项公式;(Ⅱ)若数列
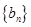 满足:
满足: ,求数列
,求数列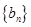 的前
的前 项和
项和 .
. 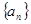 满足
满足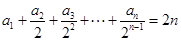 ,
,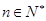 .
.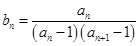 ,求数列
,求数列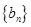 的前
的前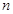 项和
项和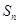 .
. 的各项均为正数,
的各项均为正数,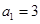 ,前
,前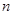 项和为
项和为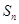 ,等比数列
,等比数列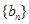 中,
中,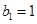 ,
,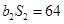 ,
,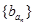 是公比为64的等比数列.
是公比为64的等比数列.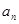 与
与 ;
; 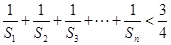 .
.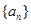 的前
的前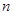 项和
项和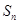 满足
满足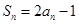 ,等差数列
,等差数列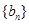 满足
满足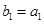 ,
,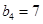 .
.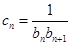 ,数列
,数列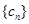 的前
的前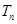 ,求证
,求证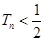 .
. ,
,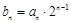 ,求数列{bn}前n项的和Tn.
,求数列{bn}前n项的和Tn.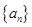 首项
首项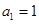 ,公差为
,公差为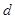 ,且数列
,且数列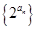 是公比为4的等比数列,
是公比为4的等比数列,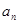 及前
及前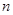 项和
项和 ;
; 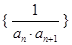 的前
的前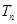 .
. 是函数
是函数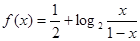 图象上任意两点,且
图象上任意两点,且 ,已知点
,已知点 的横坐标为
的横坐标为 ,且有
,且有 ,其中
,其中 且n≥2,
且n≥2, ,
, ,
,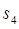 及
及 ;
;  ,其中
,其中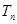 为数列
为数列 的前n项和,若
的前n项和,若 对一切
对一切 的前
的前 项和为
项和为 ,满足
,满足 ,且
,且 依次是等比数列
依次是等比数列 的前两项。
的前两项。
 且
且 ,使得数列
,使得数列 是常数列?若存在,求出
是常数列?若存在,求出 的值;若不存在,说明理由。
的值;若不存在,说明理由。