题目内容
等比数列 中,
中, ,
, ,
, 分别是下表第一、二、三行中的某一个数,且
分别是下表第一、二、三行中的某一个数,且 ,
, ,
, 中的任何两个数不在下表的同一列.
中的任何两个数不在下表的同一列.
| | 第一列 | 第二列 | 第三列 |
| 第一行 | 3 | 2 | 10 |
| 第二行 | 6 | 4 | 14 |
| 第三行 | 9 | 8 | 18 |
 的通项公式;
的通项公式;(Ⅱ)若数列
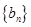 满足:
满足: ,求数列
,求数列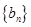 的前
的前 项和
项和 .
.
(Ⅰ) ;(Ⅱ)
;(Ⅱ) 。
。
解析试题分析:(I)当 时,不合题意;当
时,不合题意;当 时,当且仅当
时,当且仅当 时,符合题意;当
时,符合题意;当 时,不合题意.因此
时,不合题意.因此 所以公式q=3,故
所以公式q=3,故
(II)因为

所以 所以
所以
当n为偶数时,

当n为奇数时,

综上所述,
考点:等比数列的性质;等比数列的通项公式;数列前n项和的求法。
点评:本题考查的是数列求和问题.在解答的过程当中充分体现了分类讨论的思想、分组求和的方法、等比数列通项的求法以及运算能力.值得同学们体会和反思.

练习册系列答案
相关题目
设数列 的前n项和
的前n项和 ,则
,则 的值为( ).
的值为( ).
| A.15 | B.16 | C.49 | D.64 |
数列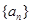 中,
中, ,
, ,则
,则 =
=
| A.3 | B.4 | C.5 | D.6 |
 满足
满足

 ,求数列
,求数列 的前n项和
的前n项和
 ,n∈N﹡,数列{bn}满足an=4log2bn+3,n∈N﹡。
,n∈N﹡,数列{bn}满足an=4log2bn+3,n∈N﹡。 的各项均为正数,
的各项均为正数,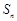 为其前
为其前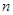 项和,对于任意
项和,对于任意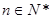 ,总有
,总有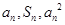 成等差数列.
成等差数列. ,数列
,数列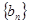 的前
的前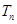 ,求证:
,求证: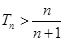 .
. 中,
中, ,
,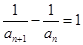 .
.  ,求
,求 的最大值。
的最大值。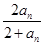 (n∈N*).
(n∈N*).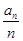 ,求数列{bn}的前n项和sn。
,求数列{bn}的前n项和sn。 ,{bn}的前n项和为Sn,求证
,{bn}的前n项和为Sn,求证