题目内容
已知数列 的前
的前 项和为
项和为 ,满足
,满足 ,且
,且 依次是等比数列
依次是等比数列 的前两项。
的前两项。
(1)求数列 及
及 的通项公式;
的通项公式;
(2)是否存在常数 且
且 ,使得数列
,使得数列 是常数列?若存在,求出
是常数列?若存在,求出 的值;若不存在,说明理由。
的值;若不存在,说明理由。
(1) ,
, ;(2)存在
;(2)存在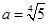
解析试题分析:(1)n=1,
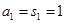

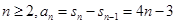

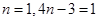

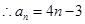

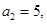


(2)存在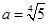 ,
, 
 为常数列,
为常数列,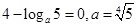
考点:本题主要考查等差数列、等比数列的通项公式,存在性问题探究。
点评:基础题,首先利用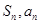 的关系,确定得到
的关系,确定得到 的通项公式,进一步得到
的通项公式,进一步得到 的通项公式。(2)作为存在性问题,从确定
的通项公式。(2)作为存在性问题,从确定 的特征入手,较为容易。
的特征入手,较为容易。

练习册系列答案
相关题目
设数列 的前n项和
的前n项和 ,则
,则 的值为( ).
的值为( ).
| A.15 | B.16 | C.49 | D.64 |
 满足
满足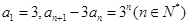 ,数列
,数列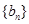 满足
满足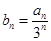 .
. 项和
项和 .
. 满足
满足

 ,求数列
,求数列 的前n项和
的前n项和
 }满足a
}满足a =2a
=2a +a
+a ,且a
,且a +a
+a =2a
=2a +4,其中n∈N
+4,其中n∈N .
. ,求数列{b
,求数列{b +
+ +…+
+…+ >
> (n≥2).
(n≥2). x
x -
- x+1=0(n∈N)有两根α和β,且满足6α-2αβ+6β=3.
x+1=0(n∈N)有两根α和β,且满足6α-2αβ+6β=3.
 的各项均为正数,且满足
的各项均为正数,且满足 ,
,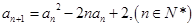 .
. 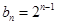 ,令
,令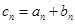 ,求数列
,求数列 的前
的前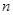 项和
项和
 ,n∈N﹡,数列{bn}满足an=4log2bn+3,n∈N﹡。
,n∈N﹡,数列{bn}满足an=4log2bn+3,n∈N﹡。 的各项均为正数,
的各项均为正数,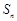 为其前
为其前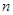 项和,对于任意
项和,对于任意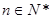 ,总有
,总有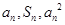 成等差数列.
成等差数列. ,数列
,数列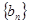 的前
的前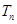 ,求证:
,求证: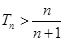 .
.