题目内容
4.已知函数f(x)=Asin(x+φ)(A>0,0<φ<π)的最大值是1,其图象经过点M($\frac{π}{3}$,$\frac{1}{2}$),则f($\frac{3π}{4}$)=-$\frac{\sqrt{2}}{2}$.分析 由已知函数f(x),得出A的值,再根据函数图象过点M,求出φ的值,即可写出f(x)的解析式,进而利用诱导公式及特殊角的三角函数值即可计算得解.
解答 解:由函数f(x)=Asin(x+φ)(A>0,0<φ<π),x∈R的最大值是1,
∴A=1;
又其图象经过点M($\frac{π}{3}$,$\frac{1}{2}$),
∴sin($\frac{π}{3}$+φ)=$\frac{1}{2}$,
∴$\frac{π}{3}$+φ=$\frac{π}{6}$+2kπ,或$\frac{π}{3}$+φ=$\frac{5π}{6}$+2kπ,k∈Z;
∴φ=-$\frac{π}{6}$+2kπ,或φ=$\frac{π}{2}$+2kπ,k∈Z;
又0<φ<π,
∴φ=$\frac{π}{2}$;
∴f(x)=sin(x+$\frac{π}{2}$)=cosx;…(4分)
∴f($\frac{3π}{4}$)=cos$\frac{3π}{4}$=-$\frac{\sqrt{2}}{2}$…(6分)
故答案为:-$\frac{\sqrt{2}}{2}$.
点评 本题考查了同角的三角函数关系与两角差的余弦公式的应用问题,也考查了三角函数的图象与性质的应用问题,属于基础题.

练习册系列答案
相关题目
14.若a=log1664,b=lg0.2,c=20.2,则( )
| A. | c<b<a | B. | b<a<c | C. | a<b<c | D. | b<c<a |
15.某市市民月收入ξ(单位:元)服从正态分布N(3000,σ2),且P(ξ<1000)=0.1962,则P(3000≤ξ≤5000)=( )
| A. | 0.3038 | B. | 0.3924 | C. | 0.6076 | D. | 0.8038 |
19.函数y=$\sqrt{x-1}$的定义域是( )
| A. | (0,+∞) | B. | (1,+∞) | C. | [0,+∞) | D. | [1,+∞) |
13.已知p:x2-4x+3≤0,q:f(x)=$\frac{{x}^{2}+1}{x}$存在最大值和最小值,则p是q的( )
| A. | 充要条件 | B. | 充分而不必要条件 | ||
| C. | 必要而不充分条件 | D. | 既不充分也不必要条件 |
14.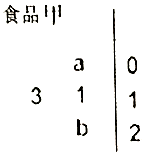 为保障春节期间的食品安全,某市质量监督局对超市进行食品检查,如图所示是某品牌食品中微量元素含量数据的茎叶图,已知该组数据的平均数为11.75,则$\frac{4}{a}+\frac{1}{b}$的最小值为( )
为保障春节期间的食品安全,某市质量监督局对超市进行食品检查,如图所示是某品牌食品中微量元素含量数据的茎叶图,已知该组数据的平均数为11.75,则$\frac{4}{a}+\frac{1}{b}$的最小值为( )
 为保障春节期间的食品安全,某市质量监督局对超市进行食品检查,如图所示是某品牌食品中微量元素含量数据的茎叶图,已知该组数据的平均数为11.75,则$\frac{4}{a}+\frac{1}{b}$的最小值为( )
为保障春节期间的食品安全,某市质量监督局对超市进行食品检查,如图所示是某品牌食品中微量元素含量数据的茎叶图,已知该组数据的平均数为11.75,则$\frac{4}{a}+\frac{1}{b}$的最小值为( )| A. | 9 | B. | $\frac{9}{2}$ | C. | 3 | D. | $\frac{7}{3}$ |
 如图,已知直三棱柱ABC-A1B1C1中,AB=AC,D为BC的中点.
如图,已知直三棱柱ABC-A1B1C1中,AB=AC,D为BC的中点.