题目内容
3.数列{an}的前n项和为Sn,$a1=2,{S_n}={a_n}({\frac{n}{3}+r})({r∈R,n∈{N^*}})$.(1)求r的值及数列{an}的通项公式;
(2)设${b_n}=\frac{n}{a_n}({n∈{N^*}})$,记{bn}的前n项和为Tn.
①当n∈N*时,λ<T2n-Tn恒成立,求实数λ的取值范围;
②求证:存在关于n的整式g(n),使得$\sum_{i=1}^{n-1}{({{T_n}+1})}={T_n}•g(n)-1$对一切n≥2,n∈N*都成立.
分析 (1)n=1时,S1=a1×$(\frac{1}{3}+r)$=a1,解得r,可得Sn=an$\frac{n+2}{3}$.利用递推关系可得$\frac{{a}_{n}}{{a}_{n-1}}$=$\frac{n+1}{n-1}$,(n≥2).利用“累乘求积”方法可得an.
(2)①bn=$\frac{n}{{a}_{n}}$=$\frac{1}{n+1}$,Tn=$\frac{1}{2}+\frac{1}{3}$+…+$\frac{1}{n+1}$,T2n=$\frac{1}{2}+\frac{1}{3}+$…+$\frac{1}{2n+1}$,作差可得数列{T2n-Tn}的单调性.利用当n∈N*时,λ<T2n-Tn恒成立,可得λ的求值范围.
②由①可得:n≥2时Tn-Tn-1=$\frac{1}{n+1}$,即(n+1)Tn-nTn-1=Tn-1+1,n≥2时,可得$\sum_{i=1}^{n-1}({T}_{i}+1)$=(n+1)Tn-1.即可得出.
解答 (1)解:n=1时,S1=a1×$(\frac{1}{3}+r)$=a1,解得r=$\frac{2}{3}$,∴Sn=an$\frac{n+2}{3}$.
n≥2时,Sn-1=an-1$•\frac{n+1}{3}$.
两式相减可得:an=an$\frac{n+2}{3}$-an-1$•\frac{n+1}{3}$.∴$\frac{{a}_{n}}{{a}_{n-1}}$=$\frac{n+1}{n-1}$,(n≥2).
∴an=$\frac{{a}_{n}}{{a}_{n-1}}$$•\frac{{a}_{n-1}}{{a}_{n-2}}$•$\frac{{a}_{n-2}}{{a}_{n-3}}$…$\frac{{a}_{3}}{{a}_{2}}$$•\frac{{a}_{2}}{{a}_{1}}•{a}_{1}$=$\frac{n+1}{n-1}$$•\frac{n}{n-2}•\frac{n-1}{n-3}$•…•$\frac{4}{2}•\frac{3}{1}$•2=n(n+1),n=1时也适合.
∴an=n(n+1).
(2)①解:bn=$\frac{n}{{a}_{n}}$=$\frac{1}{n+1}$,Tn=$\frac{1}{2}+\frac{1}{3}$+…+$\frac{1}{n+1}$,T2n=$\frac{1}{2}+\frac{1}{3}+$…+$\frac{1}{2n+1}$,
∴T2n-Tn=$\frac{1}{n+2}+\frac{1}{n+3}$+…+$\frac{1}{2n+1}$,令Bn=T2n-Tn,则Bn+1-Bn=$\frac{1}{2n+2}+\frac{1}{2n+3}$-$\frac{1}{n+2}$=$\frac{3n+4}{(2n+2)(2n+3)(n+2)}$>0,因此数列{Bn}单调递增,∴(Bn)min=$\frac{1}{3}$.
∵当n∈N*时,λ<T2n-Tn恒成立,∴$λ<\frac{1}{3}$.
②证明:由①可得:n≥2时Tn-Tn-1=$\frac{1}{n+1}$,即(n+1)Tn-nTn-1=Tn-1+1,
∴n≥2时,$\sum_{i=1}^{n-1}({T}_{i}+1)$=(3T2-2T1)+(4T3-3T2)+…+[(n+1)Tn-nTn-1]
=(n+1)Tn-2T1=(n+1)Tn-1.
∴存在关于n的整式g(n)=n+1,使得$\sum_{i=1}^{n-1}{({{T_n}+1})}={T_n}•g(n)-1$对一切n≥2,n∈N*都成立.
点评 本题考查了数列的递推关系、“累乘求积”方法、“累加求和”方法、“作差法”,考查了推理能力与计算能力,属于难题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 2016 | B. | 1680 | C. | 1344 | D. | 1008 |

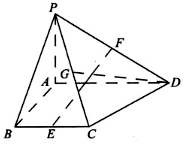 如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为直角梯形,AD∥BC,∠BAD=∠CBA=90°,PA=AB=BC=1,AD=2,E,F,G分别为BC,PD,PC的中点.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为直角梯形,AD∥BC,∠BAD=∠CBA=90°,PA=AB=BC=1,AD=2,E,F,G分别为BC,PD,PC的中点. 若某市6所中学参加中学生合唱比赛的得分用茎叶图表示如图,其中茎为十位数,叶为个位数,则这组数据的方差是$\frac{13}{3}$.
若某市6所中学参加中学生合唱比赛的得分用茎叶图表示如图,其中茎为十位数,叶为个位数,则这组数据的方差是$\frac{13}{3}$.