题目内容
已知f(x)是以π为周期的偶函数,且x∈[0,
]时,f(x)=1-sinx,则当x∈[
π,3π]时,f(x)= .
| π |
| 2 |
| 5 |
| 2 |
考点:函数解析式的求解及常用方法
专题:计算题,函数的性质及应用
分析:先由偶函数求出x∈[-
,0]时f(x)的解析式,再利用函数是以π为周期的函数得到x∈[
,3π]时f(x)的解析式.
| π |
| 2 |
| 5π |
| 2 |
解答:
解:任取x∈[-
,0],-x∈[0,
];
∵x∈[0,
]时,f(x)=1-sinx,
∴f(-x)=1+sinx;
又∵f(x)是偶函数,
∴f(-x)=f(x),
∴x∈[-
,0]时,函数f(x)=1+sinx;
∵f(x)是以π为周期的函数,
∴x当∈[
π,3π]时,x-3π∈[-
,0],
∴f(x)=f(x-3π)=1+sin(x-3π)=1-sinx;
故答案为:1-sinx.
| π |
| 2 |
| π |
| 2 |
∵x∈[0,
| π |
| 2 |
∴f(-x)=1+sinx;
又∵f(x)是偶函数,
∴f(-x)=f(x),
∴x∈[-
| π |
| 2 |
∵f(x)是以π为周期的函数,
∴x当∈[
| 5 |
| 2 |
| π |
| 2 |
∴f(x)=f(x-3π)=1+sin(x-3π)=1-sinx;
故答案为:1-sinx.
点评:本题考查了函数的周期性与奇偶性的应用问题,解题时应根据函数的性质求出解析式,是易错题.

练习册系列答案
相关题目
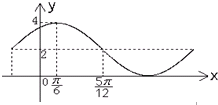 已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果
已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果