题目内容
设等差数列前n项和为Sn，前6项和为36，Sn=324,最后6项的和为180(n＞6),求数列的项数n.
解：由题意知：a1+a2+…+a6=36, ①
an+an-1+…+an-5=180, ②
①+②得：(a1+an)+(a2+an-1)+…+(a6+an-5)=6(a1+an)=36+180,
∴a1+an=36.
又Sn=
=324,
∴18n=324.∴n=18.
练习册系列答案
初中学业考试导与练系列答案
相关题目
设等差数列前n 项和为Sn，若Sm=
，Sn=
(m，n∈N* 且m≠n），则Sm+n 与4 的大小关系是（ ）
| m |
| n |
| n |
| m |
| A、Sm+n＞4 |
| B、Sm+n=4 |
| C、Sm+n＜4 |
| D、与m，n的取值有关 |
设等差数列前n项和为Sn，S10=100，S20=400，则S30等于（ ）
| A、800 | B、900 | C、1000 | D、1100 |
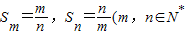且m≠n），则Sm+n 与4 的大小关系是（ ）