题目内容
设等差数列前n项和为Sn，已知a3=12，S12＞0，S13＜0，
（1）求公差d的取值范围；
（2）指出S1，S2，S3，…，S12中哪一个值最大，并说明理由。
（1）求公差d的取值范围；
（2）指出S1，S2，S3，…，S12中哪一个值最大，并说明理由。
解：（1）
，
，
，
求出
；
（2）
，
从而
，
所以S5最大。
，，，求出
；（2）
，从而
，所以S5最大。
练习册系列答案
相关题目
设等差数列前n 项和为Sn，若Sm=
，Sn=
(m，n∈N* 且m≠n），则Sm+n 与4 的大小关系是（ ）
| m |
| n |
| n |
| m |
| A、Sm+n＞4 |
| B、Sm+n=4 |
| C、Sm+n＜4 |
| D、与m，n的取值有关 |
设等差数列前n项和为Sn，S10=100，S20=400，则S30等于（ ）
| A、800 | B、900 | C、1000 | D、1100 |
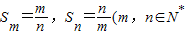且m≠n），则Sm+n 与4 的大小关系是（ ）