题目内容
8.已知圆(x-2)2+y2=4的圆心为C,过原点O的直线l与圆交于A,B两点.若△ABC的面积为1,则满足条件的直线l有( )| A. | 2条 | B. | 4条 | C. | 8条 | D. | 无数条 |
分析 根据题意画出图形,结合图形求出圆心C到直线l的距离d和弦长|AB|,
计算△ABC的面积,求出直线的斜率k的值,即可得出满足条件的直线条数.
解答 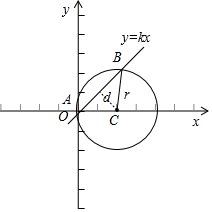 解:圆(x-2)2+y2=4的圆心为C(2,0),
解:圆(x-2)2+y2=4的圆心为C(2,0),
设过原点O的直线l为y=kx(k≠0),
则圆心C到直线l的距离为d=$\frac{|2k|}{\sqrt{{k}^{2}+1}}$,
弦长|AB|=2$\sqrt{{2}^{2}-\frac{{4k}^{2}}{{k}^{2}+1}}$;
∴△ABC的面积为
S=$\frac{1}{2}$×2$\sqrt{4-\frac{{4k}^{2}}{{k}^{2}+1}}$×$\frac{|2k|}{\sqrt{{k}^{2}+1}}$=1,
整理得k4-14k2+1=0,
解得k2=7+4$\sqrt{3}$或k2=7-4$\sqrt{3}$,
即k=±(2+$\sqrt{3}$)或k=±(2-$\sqrt{3}$);
∴满足条件的直线l有4条.
故选:B.
点评 本题考查了直线与圆的方程的应用问题,是中档题.

练习册系列答案
相关题目
16.已知实数x,y满足$\left\{\begin{array}{l}{2x-3y+6≥0}\\{x≤0}\\{y≤0}\end{array}\right.$,那么z=y-x的最大值是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 5 |
13.设△ABC的角A,B,C所对的边分别是a,b,c,若A=60°,B=75°,c=8,则a=( )
| A. | $4\sqrt{7}$ | B. | $4\sqrt{6}$ | C. | $4\sqrt{5}$ | D. | $4\sqrt{2}$ |
20.若x、y满足约束条件$\left\{\begin{array}{l}3x+y-6≤0\\ x+y≥2\\ y≤2\end{array}\right.$,则x2+y2的最小值为( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 4 | D. | 5 |
15.下列各组数,可以是钝角三角形的长的是( )
| A. | 6,7,8 | B. | 7,8,10 | C. | 2,6,7 | D. | 5,12,13 |