题目内容
函数f（x）=6cos2
+
sinωx-3（ω＞0）的最小正周期是8．
（Ⅰ）求ω的值及函数f（x）的值域；
（Ⅱ）若f（x0）=
，且x0∈（-
，
），求f（x0+1）的值．
| ωx |
| 2 |
| 3 |
（Ⅰ）求ω的值及函数f（x）的值域；
（Ⅱ）若f（x0）=
8
| ||
| 5 |
| 10 |
| 3 |
| 2 |
| 3 |
考点：三角函数中的恒等变换应用,三角函数的周期性及其求法,由y=Asin（ωx+φ）的部分图象确定其解析式
专题：三角函数的图像与性质
分析：（Ⅰ）首先，借助于二倍角公式和辅助角公式，化简函数解析式，然后，利用周期公式，确定ω的值，最后，结合三角函数的图象与性质求解函数值域；
（Ⅱ）根据（1），求解x0的值，然后，再求解f（x0+1）的值．
（Ⅱ）根据（1），求解x0的值，然后，再求解f（x0+1）的值．
解答：
解：（Ⅰ）函数f（x）=6cos2
+
sinωx-3
=3cosωx+
sinωx
=2
（
sinωx+
cosωx）
=2
sin（ωx+
）．
函数的周期是2，∴T=2，ω=
=π．
2
sin（πx+
）∈[-2
，2
]．
∴函数f（x）的值域：[-2
，2
]．
（Ⅱ）若f（x0）=
，且x0∈（-
，
），∴2
sin（πx0+
）=
．∴sin（πx0+
）=
．
f（x0+1）=2
sin（πx0+
+π）=-2
sin（πx0+
）=-
．
| ωx |
| 2 |
| 3 |
=3cosωx+
| 3 |
=2
| 3 |
| 1 |
| 2 |
| ||
| 2 |
=2
| 3 |
| π |
| 3 |
函数的周期是2，∴T=2，ω=
| 2π |
| T |
2
| 3 |
| π |
| 3 |
| 3 |
| 3 |
∴函数f（x）的值域：[-2
| 3 |
| 3 |
（Ⅱ）若f（x0）=
8
| ||
| 5 |
| 10 |
| 3 |
| 2 |
| 3 |
| 3 |
| π |
| 3 |
8
| ||
| 5 |
| π |
| 3 |
| 4 |
| 5 |
f（x0+1）=2
| 3 |
| π |
| 3 |
| 3 |
| π |
| 3 |
8
| ||
| 5 |
点评：本题综合考查了二倍角公式、辅助角公式等，注意周期公式在解题中的灵活运用，属于中档题．
练习册系列答案
相关题目
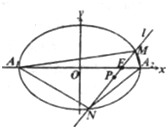已知椭圆C：
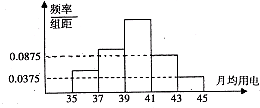某乡镇供电所为了调查农村居民用电量情况，随机抽取了500户居民去年的用电量（单位：kw/h），将所得数据整理后，画出频率分布直方图如图所示；其中直方图从左到右前3个小矩形的面积之比为1：2：3．该乡镇月均用电量在37～39之内的居民共有