题目内容
11.已知全集U=R,集合A={x|y=$\frac{1}{\sqrt{x-2}}$+lg(3-x)},集合B={x|x2+(2-a)x-2a<0}.(1)求集合C∪A.
(2)若A∪B=A,求实数a的取值范围.
分析 (1)由函数f(x)的解析式可得不等式组,由此求得函数的定义域A,从而求得∁UA.
(2)先求出集合B,若A∪B=A,则B⊆A,当B≠∅时,通过讨论a的范围,解得a的范围;当B=∅时,应有a=-2,由此解得a的范围.再把以上两个实数a的取值范围取并集,即得所求.
解答 解:(1)∵集合A={x|y=$\frac{1}{\sqrt{x-2}}$+lg(3-x)},
∴$\left\{\begin{array}{l}{x-2>0}\\{3-x>0}\end{array}\right.$ $\left\{\begin{array}{l}{x+2>0}\\{3-x>0}\end{array}\right.$,解得2<x<3,
即A=(2,3),
∴∁UA=(-∞,2]∪[3,+∞).
(2)集合B={x|x2+(2-a)x-2a<0},
∴(x+2)(x-a)<0,
a>-2时,解得:B=(-2,a),
a<-2时,解得:B=(a,-2),
a=-2时,B=∅,
若A∪B=A,则B⊆A,再根据集合B={x|a<x<2a-1},
故当B≠∅时,应有-2<a≤2或a<-2.
当B=∅时,应有a=-2.
综上可得,实数a的取值范围为(-∞,2].
点评 本题主要考查求函数的定义域,集合间的包换关系,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.下列各组函数中,表示同一函数的是( )
| A. | y=$\sqrt{{x}^{2}}$和y=$(\sqrt{x})^{2}$ | B. | y=lg(x2-1)和y=lg(x+1)+lg(x-1) | ||
| C. | y=logax2和y=2logx | D. | y=x和y=logaax |
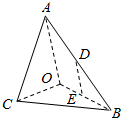 如图,在三棱锥AB0C中.AO⊥平面BOC,∠OAB=∠OAC=$\frac{π}{6}$.AB=AC=2.BC=$\sqrt{2}$,D,E分别为AB,OB的中点.
如图,在三棱锥AB0C中.AO⊥平面BOC,∠OAB=∠OAC=$\frac{π}{6}$.AB=AC=2.BC=$\sqrt{2}$,D,E分别为AB,OB的中点.