题目内容
已知正四棱锥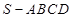 的侧棱长与底面边长都相等,
的侧棱长与底面边长都相等,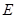 是
是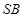 的中点,则
的中点,则 所成的角的余弦值为( )
所成的角的余弦值为( )
A. | B.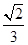 | C.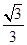 | D. |
C
解析试题分析:建立如图所示坐标系,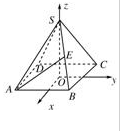
令正四棱锥的棱长为2,则A(1,-1,0),D(-1,-1,0),S(0,0,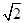 ),E(
),E(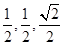 ),则
),则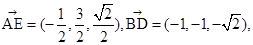 ,因此可知cos
,因此可知cos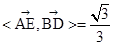 ,故选C.
,故选C.
考点:本题主要考查了多面体的结构特征和空间角的求法,同时,还考查了转化思想和运算能力,属中档题.
点评:解决该试题的关键是由于是正方体,又是求角问题,所以易选用向量量,所以建立如图所示坐标系,先求得相关点的坐标,进而求得相关向量的坐标,最后用向量夹角公式求解.

练习册系列答案
相关题目
球内接正四棱锥的高为3,体积为6,则这个球的表面积是( )
| A.16π | B.20π | C.24π | D.32π |
已知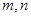 是两条不同直线,
是两条不同直线,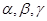 是三个不同平面,下列命题正确的( )
是三个不同平面,下列命题正确的( )
A.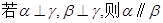 | B.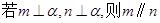 | C.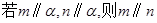 | D.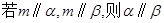 |
设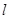 ,
, 是两条不同的直线,
是两条不同的直线, 是一个平面,则下列命题正确的是
是一个平面,则下列命题正确的是
A.若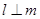 , ,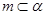 ,则 ,则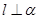 | B.若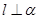 , , ,则 ,则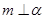 |
C.若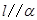 , ,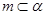 ,则 ,则 | D.若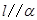 , ,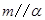 ,则 ,则 |
若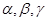 是三个互不重合的平面,
是三个互不重合的平面,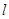 是一条直线,则下列命题中正确的是( )
是一条直线,则下列命题中正确的是( )
A.若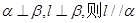 |
B.若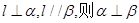 |
C.若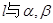 的所成角相等,则 的所成角相等,则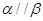 |
D.若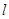 上有两个点到α的距离相等,则 上有两个点到α的距离相等,则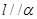 |
若直线 不平行于平面
不平行于平面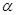 ,且
,且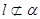 ,则( )
,则( )
A.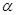 内的所有直线与 内的所有直线与 异面 异面 |
B.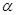 内不存在与 内不存在与 平行的直线 平行的直线 |
C.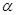 内存在唯一的直线与 内存在唯一的直线与 平行 平行 |
D.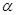 内的直线与 内的直线与 都相交 都相交 |
在正方体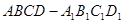 中,E是棱
中,E是棱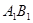 的中点,则BE与平面
的中点,则BE与平面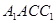 所成角的正弦值为
所成角的正弦值为
A.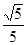 | B.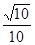 | C.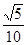 | D.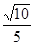 |
如图,直三棱柱 侧面
侧面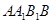 是边长为5的正方形,
是边长为5的正方形,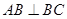 ,
,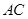 与
与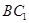 成
成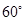 角,则
角,则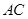 长 ( )
长 ( )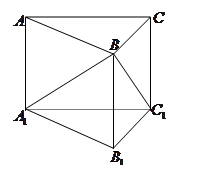
| A.13 | B.10 | C.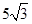 | D. |
若a,b是异面直线,且a∥平面α,则b和α的位置关系是( )
| A.平行 | B.相交 |
| C.b在α内 | D.平行、相交或b在α内 |