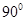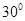题目内容
已知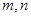 是两条不同直线,
是两条不同直线,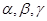 是三个不同平面,下列命题正确的( )
是三个不同平面,下列命题正确的( )
A.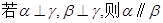 | B.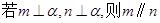 | C.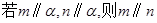 | D.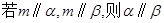 |
B
解析试题分析:对于A:若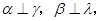 则
则 可能平行也可能相交;
可能平行也可能相交;
对于B: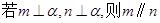 ,此为线面垂直的性质定理;
,此为线面垂直的性质定理;
对于C:若 ,则
,则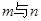 可能平行、相交或异面;
可能平行、相交或异面;
对于D:若 ,则
,则 可能平行也可能相交。因此选B。
可能平行也可能相交。因此选B。
考点:点线面之间的位置关系;线面垂直的性质定理。
点评:本题考查了空间想象能力,做题时要注意特殊情况,属于基础题型。

练习册系列答案
相关题目
正三棱锥的侧面与底面所成的角的余弦值为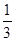 ,则侧棱与底面所成角的正弦值为( )
,则侧棱与底面所成角的正弦值为( )
A.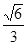 | B.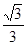 | C.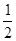 | D.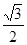 |
a、b、c为三条不重合的直线,α、β、γ为三个不重合的平面,现给出六个命题: 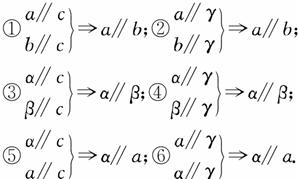
其中正确的命题是( )
| A.①②③ | B.①④⑤ | C.①④ | D.①④⑤⑥ |
如果一条直线垂直于一个平面内的①三角形的两边;②梯形的两边;③圆的两条直径;④正六边形的两条边,则能保证该直线与平面垂直的是( )
| A.①③ | B.② | C.②④ | D.①②④ |
若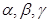 是三个互不重合的平面,
是三个互不重合的平面,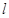 是一条直线,则下列命题中正确的是( )
是一条直线,则下列命题中正确的是( )
A.若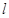 与 与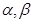 的所成角相等,则 的所成角相等,则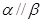 | B.若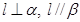 ,则 ,则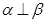 |
C.若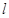 上有两个点到 上有两个点到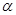 的距离相等,则 的距离相等,则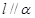 | D.若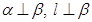 ,则 ,则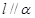 |
已知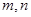 是不同的直线,
是不同的直线,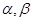 是不同的平面,给出下列命题真命题是
是不同的平面,给出下列命题真命题是
| A.若m⊥α,n⊥β,α⊥β,则m⊥n | B.若m//α,n//β,α//β,则m//n |
| C.若m⊥α,n//β,α⊥β,则m⊥n | D.若m//α,n⊥β,α⊥β,则m//n |
已知正四棱锥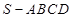 的侧棱长与底面边长都相等,
的侧棱长与底面边长都相等,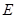 是
是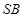 的中点,则
的中点,则 所成的角的余弦值为( )
所成的角的余弦值为( )
A. | B.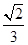 | C.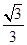 | D. |
空间四边形 中,若
中,若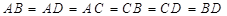 ,则
,则 与
与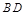 所成角为( )
所成角为( )
A. | B.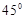 | C.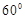 | D.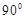 |
 侧棱长为
侧棱长为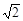 ,底面边长为
,底面边长为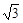 ,
, 是
是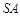 的中点,则异面直线
的中点,则异面直线 与
与 所成角的大小为( )
所成角的大小为( )