题目内容
已知sin(α-β)cosα-cos(α-β)sinα=
,β是第三象限角,求cos(β+
).
| 3 |
| 5 |
| 5π |
| 4 |
考点:两角和与差的正弦函数
专题:计算题,三角函数的求值
分析:运用两角差的正弦公式,得到sinβ=-
,由于β是第三象限角,则cosβ=-
.再由两角和的余弦公式,即可得到.
| 3 |
| 5 |
| 4 |
| 5 |
解答:
解:由sin(α-β)cosα-cos(α-β)sinα=
,
得sin(α-β-α)=
,即sin(-β)=
,
即sinβ=-
,
由于β是第三象限角,则cosβ=-
.
则cos(β+
)=cosβcos
-sinβsin
=-
×(-
)-(-
)×(-
)=
.
| 3 |
| 5 |
得sin(α-β-α)=
| 3 |
| 5 |
| 3 |
| 5 |
即sinβ=-
| 3 |
| 5 |
由于β是第三象限角,则cosβ=-
| 4 |
| 5 |
则cos(β+
| 5π |
| 4 |
| 5π |
| 4 |
| 5π |
| 4 |
=-
| ||
| 2 |
| 4 |
| 5 |
| 3 |
| 5 |
| ||
| 2 |
| ||
| 10 |
点评:本题考查两角差的正弦公式的逆用,考查同角公式,以及两角和的余弦公式,考查运算能力,属于基础题.

练习册系列答案
相关题目
在△ABC中,角A,B,C的对边分别为a,b,c,且a,b,c依次成等比数列,B=60°,则△ABC的形状为( )
| A、锐角三角形 | B、直角三角形 |
| C、等边三角形 | D、无法确定 |
函数y=x2-2x-3,x∈(-1,2]的值域( )
| A、[-3,0) |
| B、[-4,0) |
| C、(-3,0] |
| D、(-4,0] |
某班班会准备从含甲、乙的7人中选取4人发言,要求甲、乙两人至少有一人参加,且若甲、乙同时参加,则他们发言时顺序不能相邻,那么不同的发言顺序有( )
| A、720种 | B、520种 |
| C、600种 | D、360种 |
已知抛物线C:y2=x与直线l:y=kx+1,“k<0”是“直线l与抛物线C有两个不同交点”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |




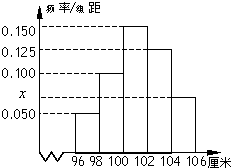 某幼儿园根据部分同年龄段女童的身高数据绘制了频率分布直方图,其中身高的变化范围是[96,106](单位:厘米),样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106].
某幼儿园根据部分同年龄段女童的身高数据绘制了频率分布直方图,其中身高的变化范围是[96,106](单位:厘米),样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106].