题目内容
18.设椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$过点(0,4)离心率为$\frac{3}{5}$(1)求C的方程;
(2)求过点(3,0)且斜率为$\frac{4}{5}$的直线被C所截线段中点坐标.
分析 (1)由题意可知:b=4,根据椭圆离心率公式即可求得b的值,求得椭圆方程;
(2)由点斜式方程求得直线AB方程,代入椭圆方程,求得A和B点坐标,利用中点坐标公式,即可求得AB的中点坐标.
解答 解:(1)由椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$过点(0,4),则b=4-------------(2分)
椭圆离心率为e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\frac{3}{5}$,则a=5,------------------(3分)
∴C的方程为$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{16}=1$;--------------------------(5分)
(2)过点(3,0)且斜率为$\frac{4}{5}$的直线方程为y=$\frac{4}{5}$(x-3),--------(6分)
设直线与C的交点为A(x1,y1),B(x2,y2),
将直线方程y=$\frac{4}{5}$(x-3)代入C的方程,得x2-3x-8=0,解得-------------------------(8分)
x1=$\frac{3-\sqrt{41}}{2}$,x2=$\frac{3+\sqrt{41}}{2}$,----------------------(9分)
∴AB的中点M(x0,y0)坐标x0=$\frac{{x}_{1}+{x}_{2}}{2}$=$\frac{3}{2}$,---------------------(10分)
y0=$\frac{{y}_{1}+{y}_{2}}{2}$=$\frac{2}{5}$(x1+x1-6)=-$\frac{6}{5}$,--------------(11分)
即中点为($\frac{3}{2}$,-$\frac{6}{5}$).--------------------------------(12分)
点评 本题考查椭圆的标准方程及简单几何性质,直线与椭圆的位置关系,中点坐标公式,考查计算能力,属于中档题.

 名校课堂系列答案
名校课堂系列答案| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
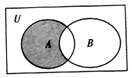 若全集U、集合A、集合B及其关系用韦恩图表示如图所示,则图中阴影表示的集合为( )
若全集U、集合A、集合B及其关系用韦恩图表示如图所示,则图中阴影表示的集合为( )| A. | ∁U(A∩B) | B. | ∁U(A∪B) | C. | A∩(∁UB) | D. | (∁UA)∩B |
| A. | 任何事件的概率总是在(0,1]之间 | |
| B. | 频率是客观存在的,与试验次数无关 | |
| C. | 随着试验次数的增加,事件发生的频率一般会稳定于概率 | |
| D. | 概率是随机的,在试验前不能确定 |
| A. | 2 | B. | 4 | C. | 8 | D. | 10 |
| A. | -$\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
| A. | (-∞,-1) | B. | (-∞,1) | C. | (-1,3) | D. | (-∞,-1)∪(3,+∞) |