题目内容

设数列{an} 的前n项和为 Sn，令Tn=
S1+S2+…+Sn
n
，称 Tn为数列 a1，a2，…，an的“理想数“，已知数列a1，a2，…，a20的“理想数“为21，那么数列2，a1，a2，…，a20 的“理想数”为（　　）
A、23B、24C、22D、20
考点：数列的求和
专题：等差数列与等比数列
分析：由数列的“理想数”的定义，可得s1+s2+…+s20的值，从而求出数列2，a1，a2，…，a20的“理想数”．
解答： 解：∵数列{an} 的前n项和为 Sn，令Tn=
S1+S2+…+Sn
n
，称 Tn为数列 a1，a2，…，an的“理想数
∴数列a1，a2，…，a20的“理想数“为T20=
S1+S2+…+S20
20
=21，
∴S1+S2+S3+…+S20=20×21，
∴数列2，a1，a2，…，a20 的“理想数”为T21=
2+(2+S1)+(2+S2)+…+(2+S20)
21
=
2×21+20×21
21
=22，
故选：C
点评：本题考查了数列的求和应用问题，解题时要认真分析，从题目中寻找解答问题的关键，从而做出解答．
练习册系列答案
相关题目
已知函数f（x）=lnx+ax+
a+1
x
．
（1）当a＞-
1
2
时，讨论f（x）的单调性；
（2）当a=1时，若关于x的不等式f（x）≥m2-5m-3恒成立，求实数m的取值范围．
下列四个命题中，正确的有（　　）个．
①?x∈R，2x2-3x+4＞0；  
②?x∈{1，-1，0}，2x+1＞0；
③?x∈N，使x2≤x；       
④?x∈N*，使x为29的约数．
A、1B、2C、3D、4
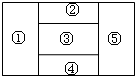如图所示，一个地区分为5个行政区域，现给地图着色，要求相邻区域不得使用同一颜色，现有4种颜色可供选择，则不同的着方法共有（　　）种．
A、36B、24C、72D、48
在数列{an}中，已知a1=2，an=2an-1（n≥2，n∈N*）．
（1）试写出a2，a3，并求数列{an}的通项公式an；
（2）设bn=log2an，求数列{bn}的前n项和Sn．
若x3=a0+a1（x-2）+a2（x-2）2+a3（x-2）3，则a2的值为（　　）
A、12B、9C、6D、3
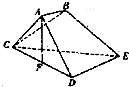已知多面体ABCDE中，AB⊥平面ACD，DE⊥平面ACD，AC=AD=CD=DE=2a，AB=a，F为CD的中点．
（1）求证：AF⊥平面CDE；
（2）求异面直线AC，BE所成角的余弦值；
（3）求多面体ABCDE的体积．
已知|
a
|=3，
a
•
b
=-12，则向量
b
在向量
a
方向上的投影的值为
 
．
已知二次函数f（x）=x2+ax+b，满足f（0）=6，f（1）=5．
（1）求函数y=f（x）的解析式；
（2）当x∈[-2，2]时，求函数y=f（x）的最小值和最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网