题目内容
11.过椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{3}}{3}$=1的左焦点F作直线交椭圆于A,B两点,且$\overrightarrow{BF}$=2$\overrightarrow{FA}$,则三角形0AB的面积是(0为坐标原点)$\frac{9\sqrt{5}}{16}$.分析 设直线AB的参数方程,代入椭圆的方程,利用韦达定理、$\overrightarrow{BF}$=2$\overrightarrow{FA}$,求出直线的斜率,可得直线的方程,即可求出三角形0AB的面积.
解答 解:F(-1,0),设直线AB的参数方程为$\left\{\begin{array}{l}{x=-1+tcosα}\\{y=tsinα}\end{array}\right.$(t为参数),
代入椭圆的方程可得3(-1+tcosα)2+4(tsinα)2=12,
化为(3+sin2α)t2-6tcosα-9=0,
∴t1+t2=$\frac{6cosα}{3+si{n}^{2}α}$,t1t2=$\frac{-9}{3+si{n}^{2}α}$.
∵t1=-2t2,
∴代入化简可得cosα=$\frac{2}{3}$,
∴tanα=$\frac{\sqrt{5}}{2}$,
∴直线AB的方程为y=$\frac{\sqrt{5}}{2}$(x+1),
∵|t1-t2|=$\frac{27}{8}$,O到直线AB的距离d=$\frac{\frac{\sqrt{5}}{2}}{\sqrt{\frac{5}{4}+1}}$=$\frac{\sqrt{5}}{3}$,
∴三角形0AB的面积是$\frac{1}{2}×\frac{27}{8}×\frac{\sqrt{5}}{3}$=$\frac{9\sqrt{5}}{16}$.
故答案为:$\frac{9\sqrt{5}}{16}$.
点评 本题考查了直线的参数方程应用、直线与椭圆相交弦长问题,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
1.为了宣传2015年10月在贵阳举行的“世界众筹大会”,“世界众筹大会”筹委会举办了“大众创业、万众创新”知识有奖问答活动,随机对市民15~65岁的人群抽样n人,回答问题统计结果如图所示:
(1)分别求出a,x的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,“世界众筹大会”筹委会决定给所抽取的6人颁发幸运奖,各组抽取的人数分别是多少?
(3)请根据频率分布直方图,估计样本数据的众数和中位数.
| 组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 | 频率分布直方图 |
| 第1组 | [15,25) | 5 | 0.5 | 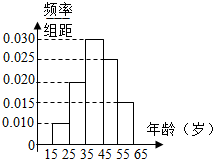 |
| 第2组 | [25,35) | a | 0.9 | |
| 第3组 | [35,45) | 27 | x | |
| 第4组 | [45,55) | 9 | 0.36 | |
| 第5组 | [55,65] | 3 | 0.2 |
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,“世界众筹大会”筹委会决定给所抽取的6人颁发幸运奖,各组抽取的人数分别是多少?
(3)请根据频率分布直方图,估计样本数据的众数和中位数.