题目内容
8.在极坐标系中,直线ρsinθ+ρcosθ=2$\sqrt{2}$被圆ρ=2$\sqrt{2}$截得的弦长为4.分析 把极坐标方程化为直角坐标方程,利用点到直线的距离公式求出弦心距,再利用弦长公式求得弦长.
解答 解:∵直线ρsinθ+ρcosθ=2$\sqrt{2}$,
∴直角坐标方程为 x+y-2$\sqrt{2}$=0,
圆ρ=2$\sqrt{2}$ 即 x2+y2=8,表示以原点为圆心、半径等于2$\sqrt{2}$的圆.
弦心距d=$\frac{|0+0-2\sqrt{2}|}{\sqrt{1+1}}$=2,可得弦长为2$\sqrt{{r}^{2}{-d}^{2}}$=2$\sqrt{8-4}$=4,
故答案为:4.
点评 本题主要考查把极坐标方程化为直角坐标方程的方法,点到直线的距离公式的应用,直线和圆的位置关系,属于基础题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
16. 某几何体的三视图如图所示,则该几何体中,最大侧面的面积为( )
某几何体的三视图如图所示,则该几何体中,最大侧面的面积为( )
 某几何体的三视图如图所示,则该几何体中,最大侧面的面积为( )
某几何体的三视图如图所示,则该几何体中,最大侧面的面积为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{6}}{2}$ |
3. 已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )
已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )
 已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )
已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )| A. | 88cm3 | B. | 104m3 | C. | 98m3 | D. | 134m3 |
14.在三棱锥P-ABC中,PA=PB=PC=6,侧棱PA与底面ABC所成的角为60°,则该三棱锥外接球的表面积为( )
| A. | 12π | B. | 24π | C. | 36π | D. | 48π |
 ,
, .
. ,求
,求 的单调区间;
的单调区间; 在
在 处取得极大值,求实数
处取得极大值,求实数 的取值范围.
的取值范围. 上是增函数的为( )
上是增函数的为( ) B.
B.
 D.
D.
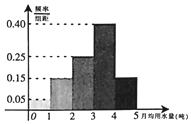 为了解某地区居民用水情况,通过抽样,获得了100位居民每人的月均用水量(单位:吨),将数据按照[0,1),[1,2)…,[4,5]分成5组,制成了如图所示的频率分布直方图.
为了解某地区居民用水情况,通过抽样,获得了100位居民每人的月均用水量(单位:吨),将数据按照[0,1),[1,2)…,[4,5]分成5组,制成了如图所示的频率分布直方图.