题目内容
已知函数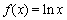 ,
,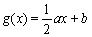 .
.
(Ⅰ)若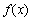 与
与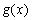 在
在 处相切,试求
处相切,试求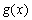 的表达式;
的表达式;
(Ⅱ)若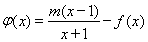 在
在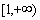 上是减函数,求实数
上是减函数,求实数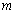 的取值范围;
的取值范围;
(Ⅲ)证明不等式: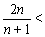
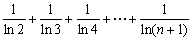
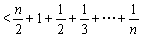 .
.
【答案】
(Ⅰ) ;(Ⅱ)
;(Ⅱ) .(Ⅲ)见解析
.(Ⅲ)见解析
【解析】
试题分析:(Ⅰ)求导数,利用 与
与 在
在 处相切,可求
处相切,可求 的表达式;(Ⅱ)
的表达式;(Ⅱ) 在
在 上是减函数,可得导函数小于等于
上是减函数,可得导函数小于等于 在
在 上恒成立,分离参数,利用基本不等式,可求实数
上恒成立,分离参数,利用基本不等式,可求实数 的取值范围;(Ⅲ)当x≥2时,证明
的取值范围;(Ⅲ)当x≥2时,证明 , 当x>1时,证明
, 当x>1时,证明  ,利用叠加法,即可得到结论.
,利用叠加法,即可得到结论.
试题解析:解:(Ⅰ)由已知 且
 得:
得: 2分
2分
又




 3分
3分
(Ⅱ)

 在
在 上是减函数,
上是减函数,
 在
在 上恒成立. 5分
上恒成立. 5分
即 在
在 上恒成立,由
上恒成立,由 ,
,

 得
得 6分
6分
(Ⅲ)由(Ⅰ)可得:当 时:
时:
 得:
得:
 8分
8分
当 时:
时: 当
当 时:
时: 当
当 时:
时:
当 时:
时: ,
,
上述不等式相加得:

即:
 ① 9分
① 9分
由(Ⅱ)可得:当 时:
时:

 在
在 上是减函数
上是减函数
 当
当 时:
时: 即
即

所以 从而得到:
从而得到: 11分
11分
当 时:
时: 当
当 时:
时: 当
当 时:
时:
当 时:
时: ,
,
上述不等式相加得:



即
 ②
②
综上:

 (
( ) 12分
) 12分
考点:1、不等式的证明;2、利用导数研究函数的单调性;3、利用导数研究曲线上某点切线方程.

练习册系列答案
相关题目
已知函数f(x)=a-
,若f(x)为奇函数,则不等式
>2的解集为( )
| 1 |
| 2x |
| f(x)+2 |
| 2x |
| A、(-∞,2) |
| B、(2,+∞) |
| C、(-∞,-2) |
| D、(-2,+∞) |